题目内容
19.符合下列条件的三角形有且只有一个的是( )| A. | a=1,b=2,c=3 | B. | b=c=1,∠B=45° | C. | a=1,b=2,∠A=100° | D. | a=1,b=$\sqrt{2},∠A={30°}$ |
分析 利用三角形中的边的关系,角的关系,及正余弦定理进行逐项分析,排除.
解答 解:对于A,由两边之和大于第三边可知符合A的三角形不存在;
对于B,由b=c=1,∠B=45°可得C=B=45°,符合条件的三角形为等腰直角三角形,符合题意;
对于C,由大边对大角原理可知B>100°,不符合三角形内角和定理;
对于D,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$得sinB=$\frac{\sqrt{2}}{2}$,∴B=45°或135°,
当B=45°时,C=105°,当B=135°时,C=15°.
∴符合条件的三角形有两个.
故选:B.
点评 本题考查了三角形的边角关系,属于基础题.

练习册系列答案
相关题目
14.若函数f(x)=x+alnx不是单调函数,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (-∞,0] | C. | (-∞,0) | D. | (0,+∞) |
4.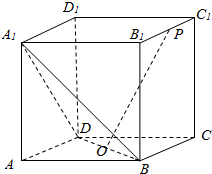 如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
 如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段B1C1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{6}}}{3},1]$ | B. | $[\frac{{\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{2}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ |
11.函数y=$\sqrt{-{x^2}+2x+8}$的单调递增区间是( )
| A. | (-∞,1) | B. | (-2,1) | C. | (1,4) | D. | (1,+∞) |
8.已知等差数列{an}为递增数列且满足a1+a10=10,则a5的取值范围是( )
| A. | (5,10) | B. | (5,+∞) | C. | (-∞,5) | D. | (10,+∞) |
9.将y=2x的图象关于直线y=x对称后,再向右平行移动一个单位所得图象表示的函数的解析式是( )
| A. | y=log2(x+1) | B. | y=log2(x-1) | C. | y=log2x+1 | D. | y=log2x-1 |