题目内容
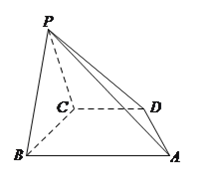
【题目】如图,P是平行四边形ABCD所在平面外一点,E是PD的中点. 
(1)求证:PB∥平面EAC;
(2)若M是CD上异于C、D的点.连结PM交CE于G,连结BM交AC于H,求证:GH∥PB.
【答案】
(1)证明:
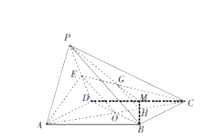
连结BD,交AC于O,
连结EO,则O是BD的中点,
又E是PD的中点,∴PB∥EO,
∵PB平面EAC,EO平面EAC,
∴PB∥平面EAC
(2)证明:由(1)知PB∥平面EAC,
又平面PBM∩平面EAC=GH,
∴根据线面平行的性质定理得:GH∥PB
【解析】(1)连结BD,交AC于O,连结EO,则PB∥EO,由此能证明PB∥平面EAC.(2)由PB∥平面EAC,根据线面平行的性质定理能证明GH∥PB.
【考点精析】认真审题,首先需要了解空间中直线与直线之间的位置关系(相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点),还要掌握直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行)的相关知识才是答题的关键.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
组别 | PM2.5浓度 | 频数(天) | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图. ①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.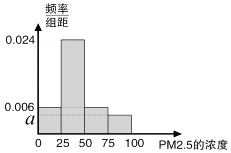
【题目】为了了解初三女生身高情况,某中学对初三女生身高情况进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中m,n,M,N所表示的数分别是多少?
(2)画出频率分布直方图;
(3)全体女生中身高在哪组范围内的人数最多?
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;
(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量K2 , 你有多大的把握认为心肺疾病与性别有关?
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)