题目内容
14.在直角坐标系中,已知A点在第一象限,B在第二象限,△AOB为等边三角形,设∠AOC=θ,C(2,0).(1)求θ的范围;
(2)用θ表示S△BOC;
(3)当θ为何值时,S△BOC最大?
分析 (1)由题意可得范围$\left\{\begin{array}{l}{0<θ<\frac{π}{2}}\\{\frac{π}{2}<θ+\frac{π}{3}<π}\end{array}\right.$,从而解得θ的范围.
(2)由题意开设等边三角形△AOB的边长为a(a>0),根据已知及三角形面积公式即可得解.
(3)由(2)及正弦函数的图象和性质即可求得最值及此时的θ值.
解答 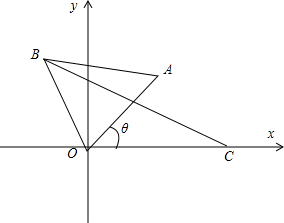 解:(1)∵A点在第一象限,B在第二象限,△AOB为等边三角形,∠AOC=θ,
解:(1)∵A点在第一象限,B在第二象限,△AOB为等边三角形,∠AOC=θ,
∴可得:$\left\{\begin{array}{l}{0<θ<\frac{π}{2}}\\{\frac{π}{2}<θ+\frac{π}{3}<π}\end{array}\right.$,解得:$\frac{π}{6}<θ<\frac{π}{2}$.
(2)∵由题意开设等边三角形△AOB的边长为a(a>0),C(2,0).
∴S△BOC=$\frac{1}{2}$OC•OB•sin∠BOC=$\frac{1}{2}×2×a×sin(θ+\frac{π}{3})$=asin($θ+\frac{π}{3}$).(a>0)
(3)由(2)可得:当$θ+\frac{π}{3}$=$\frac{π}{2}$,即θ=$\frac{π}{6}$时,S△BOC取最大值为a,(a>0).
点评 本题主要考查了三角形面积公式的应用,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
2.设函数f(x)=$\sqrt{3}$cos($\frac{π}{3}$x+$\frac{π}{2}$),若对任意x∈R都有f(x1)≥f(x)≥f(x2)成立,则|x1-x2|的最小值为( )
| A. | 6 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
19.从6件正品与3件次品中任取3件,观察正品件数与次品件数,则下列事件既是互斥事件又是对立事件的是( )
| A. | “恰好有1件次品”和“恰好有2件次品” | |
| B. | “至少有1件次品”和“全是次品” | |
| C. | “至少有1件正品”和“至多有1件次品” | |
| D. | “至少有2件次品”和“至多有1件次品” |
4.△ABC的三个内角A,B,C所对的边分别是a,b,c,设$\overrightarrow p=(a+c,b)$,$\overrightarrow q=(b-a,c-a)$,若$\overrightarrow p$∥$\overrightarrow q$,则角C的大小为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |