题目内容
2.设函数f(x)=$\sqrt{3}$cos($\frac{π}{3}$x+$\frac{π}{2}$),若对任意x∈R都有f(x1)≥f(x)≥f(x2)成立,则|x1-x2|的最小值为( )| A. | 6 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
分析 由条件根据余弦函数的值域和周期性可得|x1-x2|的最小值为函数f(x)的半个周期,计算求得结果.
解答 解:由题意可得f(x1)是f(x)的最大值,f(x2)是f(x)的最小值,
则|x1-x2|的最小值为函数f(x)的半个周期,即$\frac{1}{2}$×$\frac{2π}{\frac{π}{3}}$=3,
故选:B.
点评 本题主要考查余弦函数的值域和周期性,属于基础题.

练习册系列答案
相关题目
16.曲线y=x3在点x=2处的切线方程是( )
| A. | 12x-y-16=0 | B. | 12x+y-32=0 | C. | 4x-y=0 | D. | 4x+y-16=0 |
17.执行如图所示的程序框图,若输入n的值为2,则输出s的值是( )
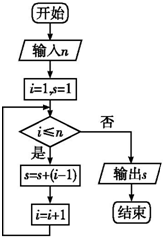

| A. | 1 | B. | 2 | C. | 4 | D. | 7 |
12.已知f(x)=2x+3x,f(x)的零点在哪个区间( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |