题目内容
8.定义:对于函数f(x),若在定义域内存在实数x0,满足f(-x0)=-f(x0),则称x0为函数f(x)的“奇对称点”.(Ⅰ)求函数f(x)=x2+2x-4的“奇对称点”;
(Ⅱ)若函数f(x)=ln(x+m)在[-1,1]上存在“奇对称点”,求实数m的取值范围.
分析 (Ⅰ)若f(x)存在“奇对称点”,则根据定义可得f(-x0)=-f(x0),代入函数解析,构造关于x0的方程,解得可得答案;
(Ⅱ)若f(x)存在“奇对称点”,则根据定义可得f(-x0)=-f(x0),代入函数解析,构造不等式,解得实数m的取值范围.
解答 解:(Ⅰ)依题意有f(-x0)=-f(x0),
即(-x0)2+2(-x0)-4=-(x0)2-2(x0)+4,…(2分)
化简得(x0)2=4,
解得:x0=±2,
∴函数f(x)=x2+2x-4的“奇对称点”为±2. …(4分)
(Ⅱ)依题意函数f(x)=ln(x+m)的定义域为(-m,+∞),…(5分)
又因为函数f(x)=ln(x+m)在[-1,1]上存在“奇对称点”,
等价于关于x的方程ln(-x+m)=-ln(x+m)在[-1,1]上有解,…(7分)
即m2=x2+1在[-1,1]上有解,…(8分)
又∵x2+1∈[1,2],…(10分)
∴$\left\{\begin{array}{l}-m<-1\\ 1≤{m}^{2}≤2\end{array}\right.$.
解得:m∈(1,$\sqrt{2}$],
实数m的取值范围为(1,$\sqrt{2}$]. …(12分)
点评 本题主要考查与函数奇偶性有关的新定义,根据条件建立方程关系是解决本题的关键,考查学生的计算能力.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
18.已知定义域为R的奇函数f(x)的导数为f′(x),当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,若a=f(1),b=-2f(-2),c=ln3f(ln3),则下列关于a,b,c的大小关系正确的是( )
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | b>c>a |
16.曲线y=x3在点x=2处的切线方程是( )
| A. | 12x-y-16=0 | B. | 12x+y-32=0 | C. | 4x-y=0 | D. | 4x+y-16=0 |
3.执行如图所示的程序框图,若输出的结果是27,则输入的数是( )
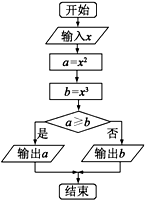

| A. | -3或-3$\sqrt{3}$ | B. | 3或-3$\sqrt{3}$ | C. | -3或3$\sqrt{3}$ | D. | 3或3$\sqrt{3}$ |
17.执行如图所示的程序框图,若输入n的值为2,则输出s的值是( )
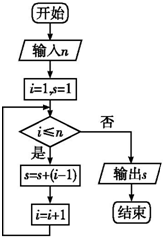

| A. | 1 | B. | 2 | C. | 4 | D. | 7 |