题目内容
5.(1)求$\frac{2π}{3}$的正弦、余弦和正切值(画图);(2)角α的终边经过点P(-3,-4),求角α的正弦、余弦和正切值.
分析 (1)利用单位圆,求出$\frac{2π}{3}$角与单位圆的交点P的坐标,利用三角函数的定义进行求解即可;
(2)由题意可得:x=-3,y=-4,故r=5,利用任意角的三角函数的定义,求出结果.
解答 解:(1)作出$\frac{2π}{3}$角与单位圆的交点P,
则P(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),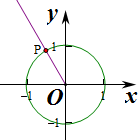
则sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,cos$\frac{2π}{3}$=-$\frac{1}{2}$,tan$\frac{2π}{3}$=$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=-$\sqrt{3}$.
(2)由题意可得:x=-3,y=-4,
∴r=$\sqrt{{x}^{2}+{y}^{2}}$=5,
sinα=$\frac{y}{r}$=-$\frac{4}{5}$,
cosα=$\frac{x}{r}$=-$\frac{3}{5}$,
tanα=$\frac{y}{x}$=$\frac{4}{3}$.
点评 本题主要考查三角函数值的计算,利用单位圆以及三角函数的定义是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.执行如图所示的程序框图,若输入n的值为2,则输出s的值是( )
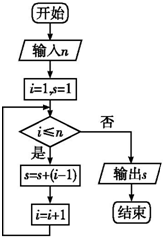

| A. | 1 | B. | 2 | C. | 4 | D. | 7 |