题目内容
3.已知数列{an}的前n项和为Sn,满足:a1=a(a≠2,a∈R),an+1=3Sn-2n+1.求证:{Sn-2n}为等比数列.分析 由an+1=Sn+1-Sn=3Sn-2n+1化简可得Sn+1-2n+1=4(Sn-2n),从而证明为等比数列即可.
解答 证明:由已知得,
an+1=Sn+1-Sn=3Sn-2n+1,
所以Sn+1=4Sn-2n+1,
所以Sn+1-2n+1=4Sn-2n+2,
所以Sn+1-2n+1=4(Sn-2n),
且S1-2=a1-2=a-2≠0,
所以{Sn-2n}是以a-2为首项,4为公比的等比数列.
点评 本题考查了等比数列的判断与应用,属于基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
17.执行如图所示的程序框图,若输入n的值为2,则输出s的值是( )
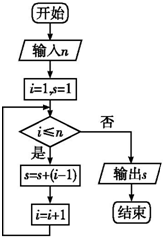

| A. | 1 | B. | 2 | C. | 4 | D. | 7 |
12.已知f(x)=2x+3x,f(x)的零点在哪个区间( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |