题目内容
已知函数 ,求导函数
,求导函数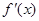 ,并确定
,并确定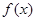 的单调区间.
的单调区间.
 ,求导函数
,求导函数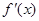 ,并确定
,并确定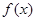 的单调区间.
的单调区间.当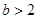 时增区间
时增区间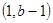 ,减区间
,减区间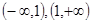 ;
;
当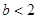 时增区间
时增区间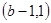 ,减区间
,减区间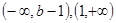 ;
;
当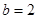 时减区间
时减区间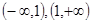 .
.
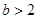 时增区间
时增区间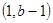 ,减区间
,减区间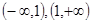 ;
;当
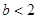 时增区间
时增区间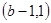 ,减区间
,减区间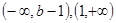 ;
;当
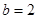 时减区间
时减区间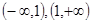 .
.本试题主要考查了含有参数的二次不等式的求解运用。首先确定定义域,然后求解导数,然后得到关于含有参数的一元二次函数,然后对于判别式记性分类讨论,确定不等式的解集,从而求解得到单调区间。当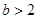 时增区间
时增区间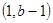 ,减区间
,减区间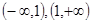
当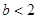 时增区间
时增区间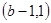 ,减区间
,减区间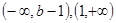
当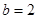 时减区间
时减区间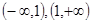
解:因为
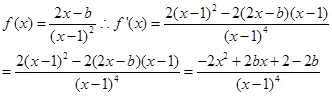
当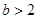 时增区间
时增区间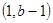 ,减区间
,减区间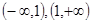
当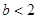 时增区间
时增区间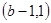 ,减区间
,减区间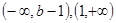
当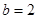 时减区间
时减区间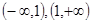
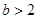 时增区间
时增区间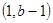 ,减区间
,减区间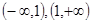
当
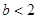 时增区间
时增区间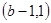 ,减区间
,减区间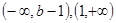
当
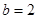 时减区间
时减区间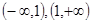
解:因为
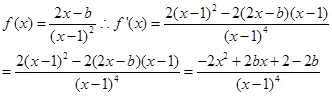
当
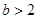 时增区间
时增区间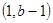 ,减区间
,减区间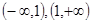
当
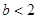 时增区间
时增区间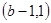 ,减区间
,减区间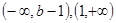
当
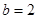 时减区间
时减区间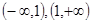

练习册系列答案
相关题目

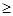 1恒成立,求a的取值集合;
1恒成立,求a的取值集合;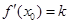 恒成立.
恒成立.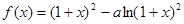 在
在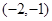 上是增函数,在
上是增函数,在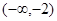 上为减函数.
上为减函数.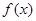 的表达式;
的表达式;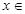
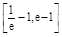 时,不等式
时,不等式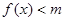 恒成立,求实数
恒成立,求实数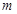 的值;
的值;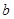 使得关于
使得关于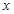 的方程
的方程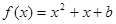 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数
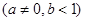 ,在区间
,在区间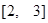 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数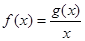 .
.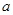 、
、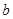 的值及函数
的值及函数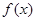 的解析式;
的解析式;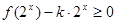 在
在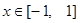 时恒成立,求实数
时恒成立,求实数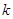 的取值范围;
的取值范围;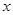 的方程
的方程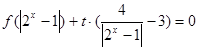 有三个相异的实数根,求实数
有三个相异的实数根,求实数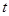 的取值范围.
的取值范围. .(
.( )
) 在区间
在区间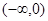 上单调递增,求实数
上单调递增,求实数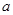 的取值范围;
的取值范围; 上,函数
上,函数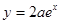 下方,求
下方,求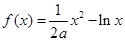 ,其中
,其中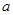 为大于零的常数.
为大于零的常数.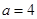 时,求函数
时,求函数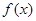 的单调区间和极值;
的单调区间和极值;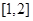 上至少存在一点
上至少存在一点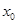 ,使得
,使得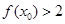 成立,求
成立,求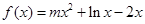 .
.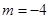 ,求函数
,求函数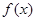 的最大值.
的最大值.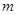 的取值范围
的取值范围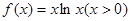 的单调递增区间是
的单调递增区间是