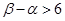题目内容
已知函数 .(
.( )
)
(1)若 在区间
在区间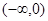 上单调递增,求实数
上单调递增,求实数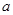 的取值范围;
的取值范围;
(2)若在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线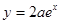 下方,求
下方,求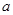 的取值范围.
的取值范围.
 .(
.( )
)(1)若
 在区间
在区间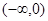 上单调递增,求实数
上单调递增,求实数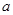 的取值范围;
的取值范围;(2)若在区间
 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线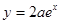 下方,求
下方,求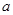 的取值范围.
的取值范围.(1) . (2)
. (2)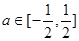 时,函数
时,函数 的图象恒在直线
的图象恒在直线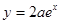 下方.
下方.
 . (2)
. (2)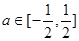 时,函数
时,函数 的图象恒在直线
的图象恒在直线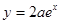 下方.
下方.第一问中,首先利用 在区间
在区间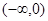 上单调递增,则
上单调递增,则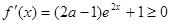 在区间
在区间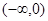 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到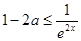 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线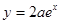 下方等价于
下方等价于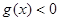 在区间
在区间 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在区间
在区间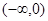 上单调递增,
上单调递增,
则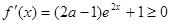 在区间
在区间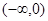 上恒成立. …………3分
上恒成立. …………3分
即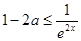 ,而当
,而当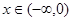 时,
时,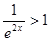 ,故
,故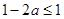 . …………5分
. …………5分
所以 . …………6分
. …………6分
(2)令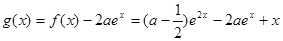 ,定义域为
,定义域为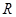 .
.
在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线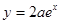 下方等价于
下方等价于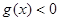 在区间
在区间 上恒成立.
上恒成立.
∵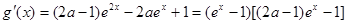 …………9分
…………9分
① 若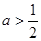 ,令
,令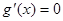 ,得极值点
,得极值点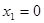 ,
,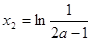 ,
,
当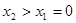 ,即
,即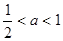 时,在(
时,在( ,+∞)上有
,+∞)上有 ,此时
,此时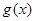 在区间
在区间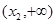 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有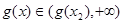 ,不合题意;
,不合题意;
当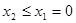 ,即
,即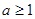 时,同理可知,
时,同理可知,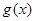 在区间
在区间 上递增,
上递增,
有 ,也不合题意; …………11分
,也不合题意; …………11分
② 若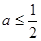 ,则有
,则有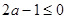 ,此时在区间
,此时在区间 上恒有
上恒有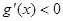 ,从而
,从而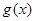 在区间
在区间 上是减函数;
上是减函数;
要使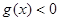 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足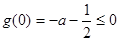
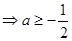 ,
,
由此求得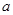 的范围是
的范围是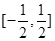 . …………13分
. …………13分
综合①②可知,当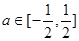 时,函数
时,函数 的图象恒在直线
的图象恒在直线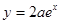 下方.
下方.
 在区间
在区间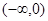 上单调递增,则
上单调递增,则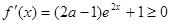 在区间
在区间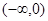 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到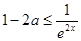 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线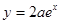 下方等价于
下方等价于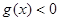 在区间
在区间 上恒成立.然后求解得到。
上恒成立.然后求解得到。解:(1)
 在区间
在区间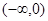 上单调递增,
上单调递增,则
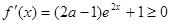 在区间
在区间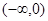 上恒成立. …………3分
上恒成立. …………3分即
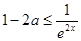 ,而当
,而当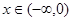 时,
时,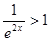 ,故
,故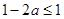 . …………5分
. …………5分所以
 . …………6分
. …………6分(2)令
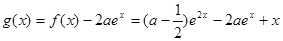 ,定义域为
,定义域为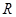 .
. 在区间
 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线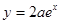 下方等价于
下方等价于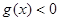 在区间
在区间 上恒成立.
上恒成立. ∵
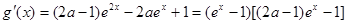 …………9分
…………9分① 若
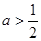 ,令
,令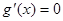 ,得极值点
,得极值点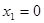 ,
,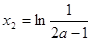 ,
,当
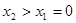 ,即
,即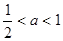 时,在(
时,在( ,+∞)上有
,+∞)上有 ,此时
,此时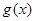 在区间
在区间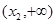 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有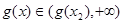 ,不合题意;
,不合题意;当
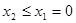 ,即
,即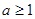 时,同理可知,
时,同理可知,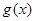 在区间
在区间 上递增,
上递增,有
 ,也不合题意; …………11分
,也不合题意; …………11分② 若
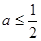 ,则有
,则有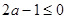 ,此时在区间
,此时在区间 上恒有
上恒有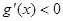 ,从而
,从而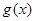 在区间
在区间 上是减函数;
上是减函数;要使
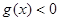 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足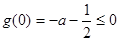
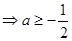 ,
,由此求得
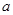 的范围是
的范围是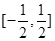 . …………13分
. …………13分综合①②可知,当
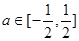 时,函数
时,函数 的图象恒在直线
的图象恒在直线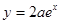 下方.
下方.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
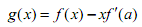 ,其中
,其中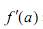 表示函数f(x)在
表示函数f(x)在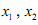 ,且
,且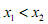 ,证明:
,证明: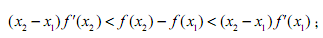
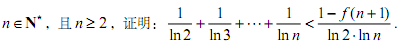
 ,
,  .
.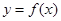 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围; 在区间
在区间 内有两个不同的零点?若存在,请求出
内有两个不同的零点?若存在,请求出 有极值,则导函数
有极值,则导函数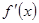 的图象不可能是 ( )
的图象不可能是 ( )
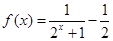 .
.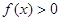 ,求实数
,求实数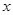 的取值范围;
的取值范围;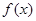 的奇偶性,并说明理由.
的奇偶性,并说明理由. ,求导函数
,求导函数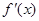 ,并确定
,并确定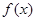 的单调区间.
的单调区间.
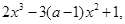 其中
其中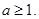
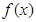 的单调区间;
的单调区间;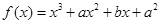 在
在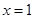 时有极值10,则实数
时有极值10,则实数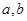 的值是( )
的值是( )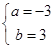

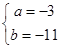 或
或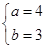
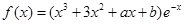
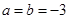 ,求
,求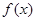 的单调区间;
的单调区间;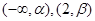 单调增加,在
单调增加,在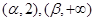 单调减少,
单调减少,