题目内容

7．在正项等比数列{an}中，a3•a6+a2•a7=2e4 则lna1•lna8的最大值为4．

分析 由等比数列性质知a1•a8=e4，再利用基本不等式，即可求出lna1•lna8的最大值．

解答 解：∵a3•a6+a2•a7=2e4，
∴由等比数列性质知a1•a8=e4，
∴lna1•lna8≤$（\frac{ln{a}_{1+}ln{a}_{8}}{2}）^{2}$=$（\frac{ln{e}^{4}}{2}）^{2}$=4，
当a1=a8=e2时取等号．
故答案为：4．

点评 本题考查等比数列性质、基本不等式的运用，考查学生分析解决问题的能力，比较基础．

练习册系列答案
相关题目
17．某地举行了一场小型公车拍卖会，轿车拍卖成交了4辆，成交价格分别为3万元，x万元，7万元，9万元；货车拍卖成交了2辆，成交价格分别为7万元，8万元．总平均成交价格为7万元．
（I）求该场拍卖会成交价格的中位数；
（Ⅱ）某人拍得两辆车，求拍得轿车、货车各一辆且总成交价格不超过14万元的概率．
18．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}-2，x≤0}\\{3x-2，x＞0}\end{array}\right.$，设集合A={y|y=|f（x）|，-1≤x≤1}，B={y|y=ax，-1≤x≤1}，若对同一x的值，总有y1≥y2，其中y1∈A，y2∈B，则实数a的取值范围是[-1，0]．
15．已知二次函数f（x）=ax2+（2b+1）x-a-2在区间[3，4]上至少有一个零点，则a2+b2的最小值为$\frac{1}{100}$．
2．阅读下面程序框图，为使输出的数据为11，则①处应填的数字可以为（　　）
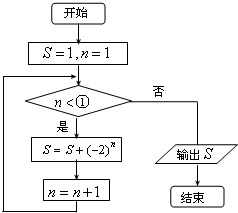
A．4B．5C．6D．7
12．不等式|x-2|+|x+3|≥7的解集是（-∞，-4]∪[3，+∞）．
19．已知△ABC的内角A，B，C的对边分别是a，b，c，且a2=b2+c2-bc．
（Ⅰ）求角A的大小；
（Ⅱ）若a=$\sqrt{3}$，求b+c的取值范围．
16．有2位女生，3位男生站成一排合影，要求女生甲不在队伍两端，3位男生中有且仅有2位相邻，则不同的排队方法共有48种．
17．已知某几何体的三视图如图所示，其中俯视图是扇形，则该几何体的体积为（　　）
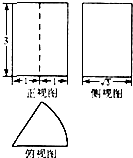
A．4 πB．2 πC．$\frac{4π}{3}$D．$\frac{2π}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网