题目内容

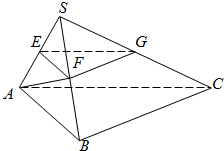
在直三棱柱ADE-BCF中，∠ADE=90°，AD=AE=EF=2，M，N分别是AF，BC的中点．
（1）求证：MN∥平面CDEF；
（2）求多面体A-CDEF的体积V．
（1）证明：连接BF，则BF过M点，连接CF，取CF的中点G，连NG

在△CBF中，NG∥FM，NG=FM
∴四边形MNGF为平行四边形，∴MN∥GF
又∵GF?平面CDEF，MN?平面CDEF
∴MN∥平面CDEF
（2）过A点作AP⊥DF于P点，则P为DF的中点，∴AP⊥DF
∵三棱柱为直棱柱
∴AP⊥面CDEF
∴多面体A-CDEF的体积V=
1
3
×2×2
2
×
2
=
8
3
．
练习册系列答案
相关题目
在矩形ABCD中，AB=3，BC=4，PA⊥平面ABCD，且PA=1，PE⊥BD，E为垂足，则PE的长为______．
如图，长方体ABCD-A1B1C1D1中，AB=3，BC=2，BB1=4，E为AD的中点，点P在线段C1E上，则点P到直线BB1的距离的最小值为（　　）
A．2B．
10
C．
3
10
5
D．
2
5
5
如果直线l是平面α的斜线，那么在平面α内（　　）
A．不存在与l平行的直线
B．不存在与l垂直的直线
C．与l垂直的直线只有一条
D．与l平行的直线有无穷多条
已知在四棱锥P一ABCD中，底面ABCD是矩形，PA⊥平面ABCD，
PA=AD=1，AB=2，E、F分别是AB、PD的中点．
（Ⅰ）求证：AF∥平面PEC；
（Ⅱ）求PC与平面ABCD所成角的正切值；
（Ⅲ）求二面角P-EC-D的正切值．
已知四棱锥S-ABCD，底面为正方形，SA⊥底面ABCD，AB=AS=a，M、N分别为AB、SC中点．
（Ⅰ）求四棱锥S-ABCD的表面积；
（Ⅱ）求证：MN∥平面SAD．
如图，已知四棱锥P-ABCD，底面ABCD为矩形，侧棱PA⊥平面ABCD，其中BC=2AB=2PA=6，M、N为侧棱PC上的两个三等分点．
①求证：AN∥平面MBD；
②求二面角M-BD-C的余弦值．
如图，在三棱锥S-ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．求证：
（1）平面EFG∥平面ABC；
（2）BC⊥SA．
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6．D、E分别是AC、AB上的点，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．
（1）求证：BC∥平面A1DE；
（2）求证：BC⊥平面A1DC；
（3）当D点在何处时，A1B的长度最小，并求出最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网