题目内容
19.把极坐标系下的点坐标(4,$\frac{π}{4}$)化为直角坐标系下的点坐标为( )| A. | (2,2$\sqrt{2}$) | B. | (2$\sqrt{2}$,2) | C. | (2$\sqrt{2}$,2$\sqrt{2}$) | D. | (1,0) |
分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出.
解答 解:∵$x=4cos\frac{π}{4}$=2$\sqrt{2}$,y=$4sin\frac{π}{4}$=2$\sqrt{2}$.
∴极坐标系下的点坐标(4,$\frac{π}{4}$)化为直角坐标系下的点坐标为$(2\sqrt{2},2\sqrt{2})$.
故选:C.
点评 本题考查了极坐标化为直角坐标的方法,属于基础题.

练习册系列答案
相关题目
13.已知y=ksinx+1,x∈R,则y的最大值为$\left\{\begin{array}{l}{k+1,k>0}\\{1,k=0}\\{-k+1,k<0}\end{array}\right.$.
7.为了创建全国卫生城市,在湛江市民中选8名青年志愿者,其中有3名男青年志愿者,5名女青年志愿者,现从中选3人参加“创建全国卫生城市”户外活动导引工作,则这3人中既有男青年志愿者又有女青年志愿者的概率为( )
| A. | $\frac{45}{512}$ | B. | $\frac{75}{512}$ | C. | $\frac{15}{64}$ | D. | $\frac{45}{56}$ |
14.已知数列{an}满足a1=2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$(n∈N*),则a1a2a3…a2012的值为( )
| A. | 2 | B. | -3 | C. | $-\frac{1}{2}$ | D. | 1 |
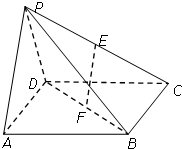 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.