题目内容
18.已知点P在曲线y=x3-x+$\frac{2}{3}$上移动,设点P处切线的倾斜角为α,则α的取值范围是( )| A. | [0,$\frac{π}{2}$] | B. | [0,$\frac{π}{2}$]∪(-$\frac{π}{2}$,0) | C. | [$\frac{3π}{4}$,π] | D. | [0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π) |
分析 根据导数的几何意义可知切线的斜率即为该点处的导数,再根据导数的取值范围求出斜率的范围,最后再根据斜率与倾斜角之间的关系k=tanα,求出α的范围即可.
解答 解:∵tanα=3x2-1,
∴tanα∈[-1,+∞).
当tanα∈[0,+∞)时,α∈[0,$\frac{π}{2}$);
当tanα∈[-1,0)时,α∈[,π).
∴α∈[0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π),
故选:D.
点评 查学生会利用导数求曲线上过某点切线方程的斜率,会利用切线的斜率与倾斜角之间的关系k=tanα进行求解.

练习册系列答案
相关题目
6.E、F分别是边长为1的正方形ABCD边BC、CD的中点,沿线AF,AE,EF折起来,则所围成的三棱锥的体积为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
7.C${\;}_{3}^{0}$+C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+C${\;}_{6}^{3}$+…+C${\;}_{20}^{17}$的值为( )
| A. | C${\;}_{21}^{3}$ | B. | C${\;}_{20}^{3}$ | C. | C${\;}_{20}^{4}$ | D. | C${\;}_{21}^{4}$ |
8.AB是圆O内的一条弦,圆O半径是5,且圆心到AB的距离为3,则弦AB的长度为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
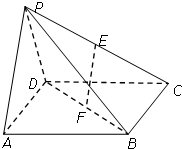 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.