题目内容
1.已知角α的顶点在坐标原点上,角α的始边与x轴的正半轴重合,并且角α的终边在射线y=-2x(x≤0)上,则cosα=$-\frac{{\sqrt{5}}}{5}$.分析 利用三角函数的定义取点(-1,2),进行求解即可.
解答 解:∵角α的终边在射线y=-2x(x≤0)上,
∴取点P(-1,2),
则r=|OP|=$\sqrt{(-1)^{2}+{2}^{2}}$=$\sqrt{5}$,
则cosα=$\frac{x}{r}=\frac{-1}{\sqrt{5}}$=$-\frac{{\sqrt{5}}}{5}$,
故答案为:$-\frac{{\sqrt{5}}}{5}$.
点评 本题主要考查三角函数求值,利用三角函数的定义是解决本题的关键.

练习册系列答案
相关题目
16.命题“?x∈R,x2+x+1>0”的否定为( )
| A. | ?x∈R,x2+x+1≤0 | B. | ?x∉R,x2+x+1≤0 | ||
| C. | ?x0∉R,x02+x0+1>0 | D. | ?x0∈R,x02+x0+1≤0 |
6.E、F分别是边长为1的正方形ABCD边BC、CD的中点,沿线AF,AE,EF折起来,则所围成的三棱锥的体积为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
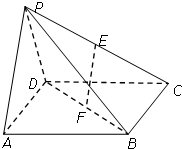 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.