题目内容
20.已知:函数f(x)=$\sqrt{2}$(sinx-cosx).(1)求函数f(x)的最小正周期和当x∈(-$\frac{π}{12}$,π)时的值域;
(2)若函数f(x)的图象过点(a,$\frac{6}{5}$),$\frac{π}{4}$<a<$\frac{3π}{4}$.求f($\frac{π}{4}$+a)的值.
分析 (1)由三角函数中的恒等变换应用化简可得解析式f(x)=2sin(x-$\frac{π}{4}$),可求函数的最小正周期为2π,由$x∈({-\frac{π}{12},π})$,可求x-$\frac{π}{4}$的范围,利用正弦函数的图象和性质即可求得当x∈(-$\frac{π}{12}$,π)时的值域.
(2)依题意得:2sin($α-\frac{π}{4}$)=$\frac{6}{5}$,可得sin($α-\frac{π}{4}$)=$\frac{3}{5}$,结合范围$\frac{π}{4}$<a<$\frac{3π}{4}$,可求0<$α-\frac{π}{4}$<$\frac{π}{2}$,可求cos($α-\frac{π}{4}$)=$\sqrt{1-si{n}^{2}(α-\frac{π}{4})}$的值,由f($\frac{π}{4}+α$)=2sin[($α-\frac{π}{4}$)+$\frac{π}{4}$],利用两角和的正弦函数公式即可求值.
解答 (本题满分14分)
解:(1)f(x)=$\sqrt{2}$(sinx-cosx)=2($\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx)=2sin(x-$\frac{π}{4}$),---(2分)
∴函数的最小正周期为2π,--------------(3分)
∵$x∈({-\frac{π}{12},π})$
$\begin{array}{l}∴x-\frac{π}{4}∈({-\frac{π}{3},\frac{3}{4}π})∴sin(x-\frac{π}{4})∈({-\frac{{\sqrt{3}}}{2},1}]\\∴y∈({-\sqrt{3},2}]\end{array}$,------------------------------(7分)
(2)依题意得:2sin($α-\frac{π}{4}$)=$\frac{6}{5}$,可得sin($α-\frac{π}{4}$)=$\frac{3}{5}$,
∵$\frac{π}{4}$<a<$\frac{3π}{4}$,
∴0<$α-\frac{π}{4}$<$\frac{π}{2}$,
∴cos($α-\frac{π}{4}$)=$\sqrt{1-si{n}^{2}(α-\frac{π}{4})}$=$\sqrt{1-(\frac{3}{5})^{2}}$=$\frac{4}{5}$,----------------------------(9分)
∵f($\frac{π}{4}+α$)=2sin[($α-\frac{π}{4}$)+$\frac{π}{4}$],--------------------------(10分)
∵sin[($α-\frac{π}{4}$)+$\frac{π}{4}$]=sin($α-\frac{π}{4}$)cos$\frac{π}{4}$+cos($α-\frac{π}{4}$)sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}(\frac{3}{5}+\frac{4}{5})$=$\frac{7\sqrt{2}}{10}$,…(13分)
∴f($\frac{π}{4}+α$)=$\frac{7\sqrt{2}}{5}$.--------------------------------------------------(14分)
点评 本题主要考查了三角函数中的恒等变换应用,两角和的正弦函数公式的应用,正弦函数的图象和性质,属于基本知识的考查.

| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,2)∪(2,+∞) |
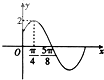 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.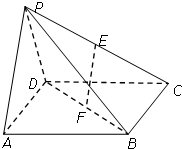 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$a.