题目内容
(14分)
已知椭圆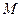 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0,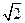 ),(0,
),(0,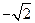 ),又点
),又点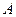
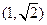 在椭圆
在椭圆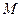 上.
上.
(1)求椭圆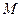 的方程;
的方程;
(2)已知直线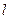 的斜率为
的斜率为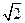 ,若直线
,若直线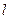 与椭圆
与椭圆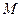 交于
交于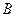 、
、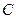 两点,求
两点,求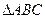 面积的最大值.
面积的最大值.
已知椭圆
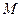 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0,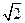 ),(0,
),(0,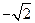 ),又点
),又点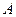
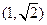 在椭圆
在椭圆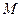 上.
上.(1)求椭圆
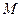 的方程;
的方程;(2)已知直线
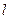 的斜率为
的斜率为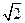 ,若直线
,若直线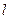 与椭圆
与椭圆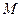 交于
交于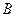 、
、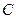 两点,求
两点,求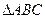 面积的最大值.
面积的最大值.(1)
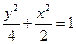
(2)
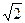
解: (Ⅰ)由已知抛物线的焦点为
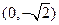 ,故设椭圆方程为
,故设椭圆方程为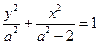 .
.将点
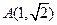 代入方程得
代入方程得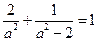 ,整理得
,整理得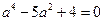 ,
,解得
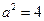 或
或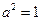 (舍).故所求椭圆方程为
(舍).故所求椭圆方程为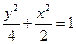 .
. (Ⅱ)设直线
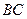 的方程为
的方程为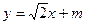 ,设
,设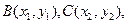
代入椭圆方程并化简得
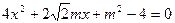 ,
, 由
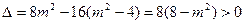 ,可得
,可得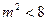 ①.
①. 由
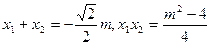 ,
,故

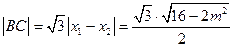 .
. 又点
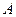 到
到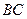 的距离为
的距离为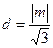 ,
, 故
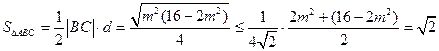 ,
,当且仅当
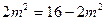 ,即
,即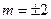 时取等号(满足①式)(基本不等式)
时取等号(满足①式)(基本不等式)所以
 面积的最大值为
面积的最大值为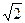 .
. 
练习册系列答案
相关题目
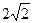 ,0)和F2(
,0)和F2(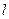 交椭圆C于A
交椭圆C于A B两点,且线段AB的中点坐标是P(-
B两点,且线段AB的中点坐标是P(-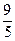 ,
,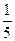 ),求直线
),求直线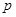 是椭圆
是椭圆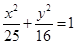 上的点.若
上的点.若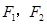 是椭圆的两个焦点,则
是椭圆的两个焦点,则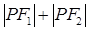 等于( )
等于( )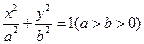 的左、右焦点为
的左、右焦点为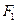 、
、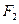 ,离心率为
,离心率为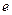 。直线
。直线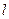 :
: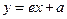 与
与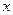 轴、
轴、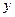 轴分别交于点A、B,M是直线
轴分别交于点A、B,M是直线 椭圆C的一个公共点,P是点
椭圆C的一个公共点,P是点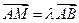 。
。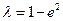
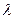 的值,使得
的值,使得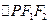 是等腰三角形。
是等腰三角形。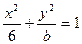 (
(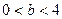 ),抛物线方程为
),抛物线方程为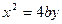 .过抛物线的焦点作
.过抛物线的焦点作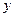 轴的垂线,与抛物线在第一象限的交点为
轴的垂线,与抛物线在第一象限的交点为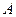 ,抛物线在点
,抛物线在点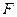 .
. 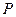 为椭圆上的动点,由
为椭圆上的动点,由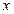 轴作垂线
轴作垂线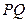 ,垂足为
,垂足为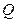 ,且直线
,且直线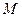 满足
满足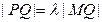 ,求点
,求点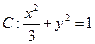 的两个焦点为
的两个焦点为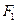 、
、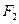 ,点
,点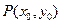 满足
满足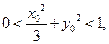 则
则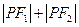 的取值范围为 ,直线
的取值范围为 ,直线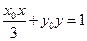 与椭圆
与椭圆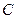 的公共点的个数为
的公共点的个数为 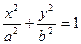 (
(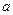
 ),篮球与地面的接触点为H,则|OH|= .
),篮球与地面的接触点为H,则|OH|= .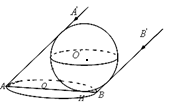
 的两个焦点为
的两个焦点为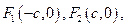
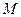 是椭圆上一点,且满
是椭圆上一点,且满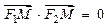 .
.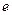 的取值
的取值 范围;
范围;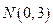 到椭圆上点的最远距离为
到椭圆上点的最远距离为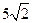 .
.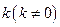 的直线
的直线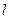 与椭圆G相交于不同两点
与椭圆G相交于不同两点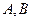 ,
,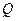 为
为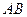 的中点,问:
的中点,问:
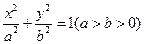 的左,右焦点为
的左,右焦点为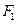 ,
,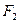 ,(1,
,(1,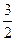 )为椭圆上一点,椭圆的
)为椭圆上一点,椭圆的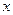 轴的对称点记为M,设
轴的对称点记为M,设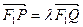 .
.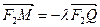 ;
;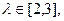 求|PQ|的取值范围
求|PQ|的取值范围