题目内容
13.若不等式(1-x)eax<1+x在x∈(0,1)上恒成立,则实数a的取值范围为(-∞,2].分析 将原不等式变形即为ln$\frac{1+x}{1-x}$-ax>0在x∈(0,1)上恒成立.令f(x)=ln$\frac{1+x}{1-x}$-ax(0<x<1),求出导数,对a讨论,当a≤2时,当a>2时,运用单调性,即可得到a的范围.
解答 解:不等式(1-x)eax<1+x在x∈(0,1)上恒成立,
即为eax<$\frac{1+x}{1-x}$,即ax<ln$\frac{1+x}{1-x}$,
即ln$\frac{1+x}{1-x}$-ax>0在x∈(0,1)上恒成立.
令f(x)=ln$\frac{1+x}{1-x}$-ax(0<x<1),
f′(x)=$\frac{2}{1-{x}^{2}}$-a,
由0<x<1可得$\frac{2}{1-{x}^{2}}$>2,
当a≤2时,f′(x)>0恒成立,即有f(x)>f(0)=0;
当a>2时,f′(x)>0不恒成立,故舍去.
综上可得a的取值范围是(-∞,2].
故答案为:(-∞,2].
点评 本题考查不等式的恒成立问题的解法,注意运用导数判断单调性,运用单调性是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.下表提供了某厂生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehaty$=$\hat b$x+$\hat a$;
(2)请求出相关指数R2,并说明残差变量对预报变量的影响约占百分之几.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请求出相关指数R2,并说明残差变量对预报变量的影响约占百分之几.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
4.已知点M(x,y)满足$\left\{\begin{array}{l}x≥1\\ x-y+1≥0\\ 2x-y-2≤0.\end{array}\right.$若ax+y的最小值为3,则a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.已知a、b为异面直线,若c∥a,则c与b的位置关系是( )
| A. | 相交 | B. | 异面 | C. | 平行 | D. | 相交或异面. |
18.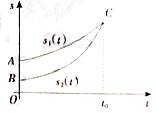 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )| A. | v甲>v乙 | B. | v甲<v乙 | C. | v甲=v乙 | D. | 大小关系不确定 |
2.计算i2=( )
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |