题目内容
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy 中，曲线C的参数方程为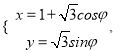
(
是参数,0≤
≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线C 的极坐标方程；
(Ⅱ)直线l1,的极坐标方程是2psin(θ+
)+
=0,直线l2:θ =
与曲线C的交点为P，与直线l1的交点为Q,求线段PQ的长.
【答案】(Ⅰ)p2-2pcosθ-2=0,其中0≤θ≤π.(Ⅱ) 5.
【解析】试题分析：(Ⅰ)曲线
的参数方程消去参数
，能求出曲线
的普通方程，再由
，能求出曲线
的极坐标方程；(Ⅱ)设
， 
，列出方程组求出
， 
，由
得出结果.
试题解析：(Ⅰ)曲线
的普通方程为
，其中
.
又∵
∴曲线
的极坐标方程为
，其中
.
(Ⅱ)设
,则
解得
， 
；
设
，则
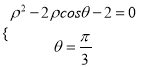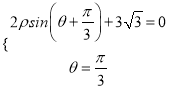解得
， 
.
故所求
.
练习册系列答案
名校课堂系列答案
相关题目
