��Ŀ����
18�����ڡ�ABC���������ĸ����⣺����sin2A=sin2B�����ABCΪ���������Σ�
����sinB=cosA�����ABC��ֱ��������
����sin2A+sin2B��sin2C�����ABC�Ƕ۽�������
����$\frac{a}{cos\frac{A}{2}}$=$\frac{b}{cos\frac{B}{2}}$=$\frac{c}{cos\frac{C}{2}}$�����ABC�ǵȱ������Σ�
������ȷ�����������Ǣۢܣ�
���� �پٷ�����2A=��-2B��
�ھٷ�����B=��-$\frac{��}{2}$+A��
�ۢ��������Ҷ�����֤����
��� �⣺��Ҳ�п���2A=��-2B�����A+B=$\frac{��}{2}$����һ���ǵ��������Σ�
��Ҳ�п�����B=��-$\frac{��}{2}$+A��B-A=$\frac{��}{2}$����ʱ������Ϊ�۽������Σ��ʢڲ�һ����ȷ��
�ۡ�sin2A+sin2B��sin2C�������Ҷ���֪a2+b2��c2��
��cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$��0��
��Cһ��Ϊ�۽ǣ�����ȷ
�ܡ�$\frac{a}{cos\frac{A}{2}}$=$\frac{b}{cos\frac{B}{2}}$��
��sin$\frac{A}{2}$=sin$\frac{B}{2}$��
��A=B��$\frac{A}{2}$+$\frac{B}{2}$=�У����������⣩��
��A=B��
ͬ����֪B=C��
��������һ��Ϊ�ȱ������Σ�
�ʴ�Ϊ���ۢ�
���� ������Ҫ���������Ҷ�����Ӧ�ã������������Ҫѧ����ϸ�̶Ƚϸߣ�

��ϰ��ϵ�д�
 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
�����Ŀ
8����֪x��y��ȡֵ�����ʾ��
����ɢ��ͼ������y��x������أ������Իع�ֱ�߷���Ϊ$\widehat{y}$=0.95x+$\widehat{a}$����$\widehat{a}$��ֵ����2.6��
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
6���÷�֤��֤�����⡰��abc=0����a��b��c��������һ��Ϊ0��ʱ��������ȷ���ǣ�������
| A�� | ����a��b��c��ֻ��һ��Ϊ0 | B�� | ����a��b��c����Ϊ0 | ||
| C�� | ����a��b��c��Ϊ0 | D�� | ����a��b��c����Ϊ0 |
13����֪x��R+����x+$\frac{4}{{x}^{2}}$����Сֵ�ǣ�������
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
10����tan570���ֵΪ��������
| A�� | -$\frac{\sqrt{3}}{3}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\sqrt{3}$ | D�� | -$\sqrt{3}$ |
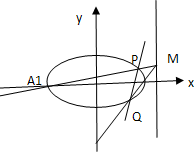 ��֪��ԲC������������ԭ�㣬������x���ϣ���Բ�ϵĵ㵽����ľ������СֵΪ2-$\sqrt{3}$����������e�Ƿ���2x2-3$\sqrt{3}$x+3=0�ĸ���
��֪��ԲC������������ԭ�㣬������x���ϣ���Բ�ϵĵ㵽����ľ������СֵΪ2-$\sqrt{3}$����������e�Ƿ���2x2-3$\sqrt{3}$x+3=0�ĸ���