题目内容
2.在△ABC中,a、b、c分别是三个内角A、B、C的对边,若向量$\overrightarrow x$=$(a,\sqrt{3}b)$与向量$\overrightarrow y=(cosA,sinB)$共线(1)求角A;
(2)若a=2,求b+c得取值范围.
分析 (1)根据向量共线的坐标条件、正弦定理进行化简,由内角的范围和特殊角的三角函数值求出角A;
(2)由(1)和正弦定理表示出b+c,利用两角和与差的正弦公式进行化简,由正弦函数的性质和角B的范围求出b+c的范围.
解答 解:(1)∵向量$\overrightarrow x$=$(a,\sqrt{3}b)$与向量$\overrightarrow y=(cosA,sinB)$共线,
∴$asinB=\sqrt{3}bcosA$,(1分)
由正弦定理得,$sinAsinB=\sqrt{3}sinBcosA$,(2分)
∵sinB>0,∴$tanA=\sqrt{3}$,(3分)
∵0<A<π,∴$A=\frac{π}{3}$;(4分)
(2)∵a=2,且$A=\frac{π}{3}$,∴$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}=\frac{4}{{\sqrt{3}}}$,(5分)
∵C=π-A-B=$\frac{2π}{3}-B$,
∴$b+c=\frac{4}{\sqrt{3}}(sinB+sinC)=\frac{4}{\sqrt{3}}(sinB+sin(\frac{2π}{3}-B))$
=$\frac{4}{\sqrt{3}}(sinB+\frac{\sqrt{3}}{2}cosB+\frac{1}{2}sinB)$=$4(\frac{\sqrt{3}}{2}sinB+\frac{1}{2}cosB)$
=$4sin(B+\frac{π}{6})$,(7分)
∵0<B<$\frac{2π}{3}$,∴$\frac{π}{6}$<$B+\frac{π}{6}$<$\frac{5π}{6}$,则$\frac{1}{2}$<$sin(B+\frac{π}{6})$≤1,(9分)
∴2<b+c≤4.(10分)
点评 本题考查正弦定理,两角和与差的正弦公式,正弦函数的性质,以及向量共线的坐标条件,注意内角的范围,属于中档题.

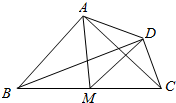 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{3}$ |