题目内容
12．由数字1，2，3，4，5组成无重复数字的五位数．（1）1、2、3按从小到大的顺序（可以不相邻）排列的五位数有多少个？
（2）比31254大的数有多少个？
（3）若把这些数按从小到大的顺序排列，第60个数是什么？
分析 （1）由数字1，2，3，4，5组成无重复数字的五位数，共有5!=120个，1、2、3的顺序，共有3！=6个，利用除法，可得结论；
（2）任何数开头的五位数有4!=24个，所以以5，4，3开头的共有72个，以3开头，比31254小的数有31245，即1个，可得结论；
（3）任何数开头的五位数有4!=24个，60=24+24+12，所以第60个数是以3开头的第12个，以3*开头的数有3！=6个，12=6+6，所以第60个数是以32开头的最末一个，即可得结论．
解答 解：（1）由数字1，2，3，4，5组成无重复数字的五位数，共有5!=120个，1、2、3的顺序，共有3！=6个，所以1、2、3按从小到大的顺序（可以不相邻）排列的五位数有20个；
（2）任何数开头的五位数有4!=24个，所以以5，4，3开头的共有72个，以3开头，比31254小的数有31245，即1个，
所以比31254大的数有70个；
（3）任何数开头的五位数有4!=24个，60=24+24+12，所以第60个数是以3开头的第12个，以3*开头的数有3！=6个，12=6+6，所以第60个数是以32开头的最末一个，即32541．
点评 本题考查排列知识的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
在平面直角坐标系xOy中，点A（-1，-2）、B（2，3）、C（-2，-1）．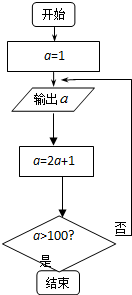
按照如图所示的框图操作，