题目内容

17．从1到2015这2015个正整数中，有多少个3的倍数？671；有多少个被3除余1且被4除余2的整数？167．

分析 从1到2015这2015个正整数中，3的倍数构成一个以3为首项，以3为公差的等差数列，其中满足条件的最大的数为2013；
被3除余1且被4除余2的整数构成一个以10为首项，以12为公差的等差数列，其中满足条件的最大的数为2014．

解答 解：从1到2015这2015个正整数中，
3的倍数构成一个以3为首项，以3为公差的等差数列，
故an=3n，其中满足条件的最大的数为2013，
当an=3n=2013时，n=671，
故从1到2015这2015个正整数中，有671个3的倍数；
被3除余1且被4除余2的整数构成一个以10为首项，以12为公差的等差数列，
故bn=12n-2，其中满足条件的最大的数为2014，
当bn=12n-2=2014时，n=167，
故从1到2015这2015个正整数中，有167个被3除余1且被4除余2的整数．
故答案为：671，167

点评 本题考查的知识点是等差数列，其中分析出满足条件的整数组成数列的公差和首项是解答的关键．

练习册系列答案
相关题目
7．已知函数$f（x）=2sinxcos（x+\frac{π}{6}）+\frac{3}{2}$．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）在锐角△ABC中，角A，B，C的对边分别为a，b，c，且满足$\frac{2b-c}{a}=\frac{cosC}{cosA}$，求f（B）的值域．
8．满足条件|z-i|+|z+i|=3的复数z在复平面上对应点的轨迹是（　　）
A．一条直线B．两条直线C．圆D．椭圆
5．函数y=2tan（3x+$\frac{π}{4}$）的周期是$\frac{π}{3}$．
12．如图是函数f（x）=x3+bx2+cx+d的大致图象，则x1+x2=（　　）
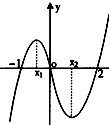
A．$\frac{2}{3}$B．$\frac{10}{9}$C．$\frac{8}{9}$D．$\frac{28}{9}$
2．在△ABC中，a、b、c分别是三个内角A、B、C的对边，若向量$\overrightarrow x$=$（a，\sqrt{3}b）$与向量$\overrightarrow y=（cosA，sinB）$共线
（1）求角A；
（2）若a=2，求b+c得取值范围．
9．已知定义在R上的函数f（x），若f（x）是奇函数，f（x+1）是偶函数，当0≤x≤1时，f（x）=x2，则f（2015）=（　　）
A．-1B．1C．0D．20152
6．某车间为了规定工时定额，需确定加工零件所花费的时间，为此进行了5次试验，收集数据如表：
加工零件数x（万个）24568
加工时间y （小时）3040605070
根据上表可得线性回归方程$\widehat{y}$=bx+a 中的b=6.5，据此模型估计加工零件10万个所需要的时间为（　　）
A．65.5小时B．72.0小时C．82.5小时D．83.0小时
7．已知$f（x）=sin（2x-\frac{π}{3}）$．
（1）求$f（{\frac{π}{8}}）$的值；         
（2）在△ABC中，角A，B，C的对边分别是a，b，c，且$f（{\frac{A}{2}}）=0$，a=3，$b+c=2\sqrt{3}$，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网