题目内容
12.已知函数f(x)=$\frac{xlnx}{x+1}$和g(x)=m(x-1)(m∈R).(1)m=1时,求方程f(x)=g(x)的实根;
(2)若对于任意的x∈[1,+∞),f(x)≤g(x)恒成立,求m的取值范围.
分析 (1)m=1时,f(x)=g(x)化为xlnx-x2+1=0,设h(x)=xlnx-x2+1,确定其单调性,即可求方程f(x)=g(x)的实根;
(2)任意的x∈[1,+∞),f′(x)=$\frac{lnx+x+1}{(x+1)^{2}}$>0,函数单调递增,f′(1)=$\frac{1}{2}$,根据对于任意的x∈[1,+∞),f(x)≤g(x)恒成立,即可求m的取值范围.
解答 解:(1)m=1时,f(x)=g(x)化为xlnx-x2+1=0,
设h(x)=xlnx-x2+1,则h′(x)=lnx+1-2x,
∴h″(x)=$\frac{1}{x}$-2,
∴h′(x)在(0,$\frac{1}{2}$)上单调递增,在($\frac{1}{2}$,+∞)上单调递减,
∴h′(x)max=h′($\frac{1}{2}$)=-ln2,
∴h′(x)<0,
∴h(x)在(0,+∞)上单调递减,
∵h(1)=0,
∴方程f(x)=g(x)的实根为x=1;
(2)∵f(x)=$\frac{xlnx}{x+1}$,
∴任意的x∈[1,+∞),f′(x)=$\frac{lnx+x+1}{(x+1)^{2}}$>0,函数单调递增,
∵f′(1)=$\frac{1}{2}$,
∴对于任意的x∈[1,+∞),f(x)≤g(x)恒成立,m≥$\frac{1}{2}$.
点评 本题考查导数知识的综合运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.已知P是△ABC所在平面外一点,若P到ABC三边距离相等,则点P在平面ABC上的射影一定是△ABC的( )
| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |
7.若E,F,G,H分别在四面体的棱AB,BC,CD,AD上,且AC∥平面EFGH,则( )
| A. | EF∥GH | B. | EH∥FG | C. | EH∥平面BCD | D. | FG∥平面ABD |
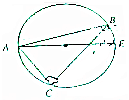 如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.
如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.