题目内容
20.已知曲线C的参数方程为$\left\{\begin{array}{l}{x=10cosφ}\\{y=8sinφ}\end{array}\right.$,(其中φ为参数)在同一平面直角坐标系中,将曲线C上的点按坐标变换$\left\{\begin{array}{l}{X=\frac{1}{5}x+3}\\{Y=\frac{1}{4}y}\end{array}\right.$得到曲线C1.(1)求曲线C1的普通方程;
(2)设点P是曲线C上的动点,过点P作直线与曲线C1切于点Q,求|PQ|的最小值.
分析 (1)利用坐标转移,代入参数方程,消去参数即可求曲线C1的普通方程;
(2)要求|PQ|的最小值,只要求出P到圆心(3,0)的距离最小值即可.
解答 解:(1)由已知得到曲线C1的参数方程为:$\left\{\begin{array}{l}{X=2cosφ+3}\\{Y=2sinφ}\end{array}\right.$,所以曲线C1的普通方程为(X-3)2+Y2=4;
(2)因为点P是曲线C上的动点,过点P作直线与曲线C1切于点Q,所以|PQ|的最小值就是P到圆心(3,0)的距离最小值为10-3=7.
点评 本题考查了参数方程和直角坐标的互化,利用直角坐标方程与参数方程间的关系,点到直线的距离公式的应用,考查计算能力.

练习册系列答案
相关题目
4.已知a>b,ab≠0,则下列不等式中:①a2>b2;②$\frac{1}{a}<\frac{1}{b}$;③a3>b3;④a2+b2>2ab,恒成立的不等式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
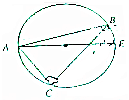 如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.
如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.