题目内容
15.设数列{an}满足an=3an-1+2(n≥2,n∈N+),且a1=2,bn=log3(an+1).(1)证明:数列{an+1}为等比数列;
(2)求数列{anbn}的前n项和Sn.
分析 (1)数列{an}满足an=3an-1+2(n≥2,n∈N+),变形为an+1=3(an-1+1),即可证明;
(2)由(1)可得:an=3n-1.由bn=log3(an+1),可得bn=$lo{g}_{3}({3}^{n}+1-1)$=n.anbn=n•(3n-1)=n•3n-n.利用“错位相减法”、等差数列与等比数列的前n项和公式即可得出.
解答 (1)证明:∵数列{an}满足an=3an-1+2(n≥2,n∈N+),
∴an+1=3(an-1+1),
∴数列{an+1}为等比数列,首项为3,公比为3;
(2)解:由(1)可得:an=3n-1.
∵bn=log3(an+1),∴bn=$lo{g}_{3}({3}^{n}+1-1)$=n.
∴anbn=n•(3n-1)=n•3n-n.
令Tn=3+2×32+3×33+…+n•3n,
∴3Tn=32+2×33+…+(n-1)•3n+n•3n+1,
∴-2Tn=3+32+…+3n-n•3n+1=$\frac{3({3}^{n}-1)}{3-1}$-n•3n+1=$\frac{1-2n}{2}$•3n+1-$\frac{3}{2}$,
∴Tn=$\frac{2n-1}{4}•{3}^{n+1}$+$\frac{3}{4}$.
∴数列{anbn}的前n项和Sn=$\frac{2n-1}{4}•{3}^{n+1}$+$\frac{3}{4}$-$\frac{n(n+1)}{2}$.
点评 本题考查了递推式的应用、等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”,考查了变形能力、推理能力与计算能力,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知过抛物线C:x2=2py(p>0)的焦点F的直线m交抛物线于点M、N,|MF|=2|NF|=3,则抛物线C的方程为( )
| A. | x2=8y | B. | x2=2y | C. | x2=4y | D. | x2=2$\sqrt{2}$y |
10.若钝角三角形ABC三内角A,B,C的度数成等差数列,且最大边长与最小边长的比为m,则m的取值范围是( )
| A. | 1<m≤2 | B. | 1<m<2 | C. | m>2 | D. | m≥2 |
20.一个几何体的三视图如图所示,则该几何体的体积为( )
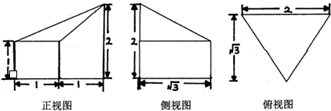

| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
7.设集合A={x|x>1},集合$B=\{x|y=\sqrt{3-x}\}$,则A∩B=( )
| A. | [0,+∞) | B. | (-∞,1) | C. | [1,+∞) | D. | (1,3] |
5.用平面在正方体上截下一个三棱锥,以原来正方体的那个顶点作为三棱锥的顶点,则该顶点在三棱锥的底面上的射影是这个三角形的( )
| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |