题目内容
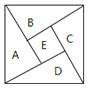
【题目】如图为我国数学家赵爽
约3世纪初
在为《周髀算经》作注时验证勾股定理的示意图，现在提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，则
区域涂色不相同的概率为
A. 
B. 
C. 
D. 
【答案】B
【解析】
利用分步计数原理求出不同的涂色方案有420种，其中，
区域涂色不相同的情况有120种，由此根据古典概型概率公式能求出区域涂色不相同的概率．
提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，
根据题意，如图，设5个区域依次为
,分4步进行
，对于区域
，有5种颜色可选；
，对于区域
与区域相邻，有4种颜色可选；
，对于区域
，与
区域相邻，有3种颜色可选；
，对于区域
，若
与颜色相同，
区域有3种颜色可选，
若与颜色不相同，区域有2种颜色可选，区域有2种颜色可选，
则区域有
种选择，
则不同的涂色方案有
种，
其中，区域涂色不相同的情况有：
，对于区域，有5种颜色可选；
，对于区域与区域相邻，有4种颜色可选；
，对于区域与
区域相邻，有2种颜色可选；
，对于区域，若与颜色相同，区域有2种颜色可选，
若与颜色不相同，区域有1种颜色可选，区域有1种颜色可选，
则区域有
种选择，
不同的涂色方案有
种，
区域涂色不相同的概率为
,故选B．
练习册系列答案
相关题目
