题目内容
3.已知△ABC的面积为3,且满足0≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6,设$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角为θ.(1)求θ的取值范围;
(2)求函数f(θ)=sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ的值域.
分析 (1)由题意可得$\frac{1}{2}$•AB•AC•sinθ=3,由0≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6,可得0≤AB•AC•cosθ≤6,求得0≤cotθ≤1,可得θ∈[$\frac{π}{4}$,$\frac{π}{2}$].
(2)利用三角恒等变换化简函数f(θ)=sin(2θ-$\frac{π}{3}$)+$\frac{1-\sqrt{3}}{2}$.由θ∈[$\frac{π}{4}$,$\frac{π}{2}$],利用正弦函数的定义域和值域,求得f(θ)的值域.
解答 解:(1)由题意可得$\frac{1}{2}$•AB•AC•sinθ=3,∴AB•AC•sinθ=6.
由0≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6,可得0≤AB•AC•cosθ≤6,故有0≤$\frac{6cosθ}{sinθ}$≤6,
求得0≤cotθ≤1,∴θ∈[$\frac{π}{4}$,$\frac{π}{2}$].
(2)函数f(θ)=sin2($\frac{π}{4}$+θ)-$\sqrt{3}$cos2θ=$\frac{1-cos(2θ+\frac{π}{2})}{2}$-$\frac{\sqrt{3}}{2}$(1+cos2θ)
=$\frac{1}{2}$+$\frac{1}{2}$sin2θ-$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$cos2θ=sin(2θ-$\frac{π}{3}$)+$\frac{1-\sqrt{3}}{2}$.
由θ∈[$\frac{π}{4}$,$\frac{π}{2}$],可得2θ-$\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],sin(2θ-$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,$\frac{3-\sqrt{3}}{2}$].
点评 本题主要考查两个向量的数量积的定义,三角恒等变换,正弦函数的定义域和值域,属于中档题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案| A. | $-\frac{π}{6}$ | B. | $\frac{π}{6}$ | C. | $-\frac{π}{12}$ | D. | $\frac{7π}{12}$ |
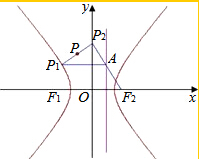 已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.
已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.