题目内容

8．已知△ABC的内角A、B、C的对边分别为a、b、c，b=3，c=1，A=2B，求a的值．

分析 利用正弦定理列出关系式，把b=3，∠A=2∠B代入得到关于a与cosB的关系式，再利用余弦定理列出关系式，把b，c，cosA=cos2B代入得到关于a与cosB的关系式，联立求出a的值即可．

解答 解：∵b=3，A=2B，
∴由正弦定理得：$\frac{a}{sinA}=\frac{b}{sinB}$，即$\frac{a}{sin2B}=\frac{3}{sinB}$，即a=6cosB，
由余弦定理得：a2=b2+c2-2bccosA=9+1-6cosA=10-6cos2B=10-6（2cos2B-1）=16-12cos2B，
把a=6cosB代入得：36cos2B=16-12cos2B，即cos2B=$\frac{1}{3}$，
∵A=2B，∴B为锐角，即cosB＞0，
∴cosB=$\frac{\sqrt{3}}{3}$，
则a=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$．

点评 此题考查了正弦、余弦定理，以及二倍角的余弦函数公式，熟练掌握正弦、余弦定理是解本题的关键．

练习册系列答案
相关题目
5．如图已知：菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直，AB=2AD=2CD=4，∠ABE=60°，∠BAD=∠CDA=90°，点H，G分别是线段EF，BC的中点．
（1）求证：平面AHC⊥平面BCE；
（2）试问在线段EF上是否存在点M，使得MG∥平面AFD，若存在求FM的长并证明，若不存在，说明理由．
6．在（$\sqrt{x}-\frac{2}{\sqrt{x}}$）n的展开式中，偶数项的二次项系数为64，则展开式共有（　　）
A．6项B．7项C．8项D．9项
3．函数f（x）=3sin（2x-$\frac{π}{6}$），在区间[0，$\frac{π}{2}$]上的值域为（　　）
A．[-$\frac{3}{2}$，$\frac{3}{2}$]B．[-$\frac{3}{2}$，3]C．[-$\frac{3\sqrt{3}}{2}$，$\frac{3\sqrt{3}}{2}$]D．[-$\frac{3\sqrt{3}}{2}$，3]
3．已知△ABC的面积为3，且满足0≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6，设$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角为θ．
（1）求θ的取值范围；
（2）求函数f（θ）=sin2（$\frac{π}{4}$+θ）-$\sqrt{3}$cos2θ的值域．
13．设函数f（x）=$\frac{{a}^{x}-1}{1{0}^{x}+1}$（a＞0且a≠1）的图象关于原点对称
（1）求实数a的值，并判断f（x）的定义域内的单调性；
（2）当θ∈[0，$\frac{π}{2}$]时，有f（cos4θ+4mtanθ$\sqrt{1-si{n}^{2}θ}$）+f（-2m-2-sin4θ）＜0恒成立，求实数m的取值范围．
20．经过A（-2，0），B（-5，3）两点的直线的倾斜角（　　）
A．45°B．135°C．90°D．60°
17．若tanθ=2，则sin2θ+sinθcosθ-2cos2θ=（　　）
A．$\frac{3}{5}$B．$\frac{4}{5}$C．$\frac{\sqrt{7}}{4}$D．$\frac{3}{4}$
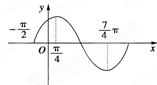18．函数f（x）=sin（ωx+φ），（|φ|＜$\frac{π}{2}$）的图象如图所示．试求：
（1）f（x）的解析式；  
（2）f（x）的单调递增区间；
（3）使f（x）取最小值的x的取值集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网