题目内容
18.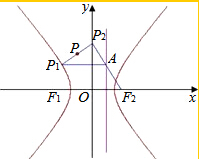 已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.
已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.(1)求线段P1P2的中点P的轨迹E的方程;
(2)设轨迹E与x轴交于B、D两点,在E上任取一点Q(x1,y1)(y1≠0),直线QB,QD分别交y轴于M,N两点.求证:以MN为直径的圆过两定点.
分析 (1)由已知得F2(3b,0),A($\frac{8}{3}$b,y0),则直线F2A的方程为:y=-$\frac{3{y}_{0}}{b}$(x-3b),令x=0得P2(0,9y0),设P(x,y),则$\left\{\begin{array}{l}{x=\frac{{x}_{0}}{2}}\\{y=\frac{{x}_{0}+9{y}_{0}}{2}=5{y}_{0}}\end{array}\right.$,由此能求出P的轨迹E的方程;
(2)在$\frac{{x}^{2}}{2{b}^{2}}$-$\frac{{y}^{2}}{25{b}^{2}}$=1中,令y=0得x2=2b2,设B,D的坐标,得到直线QD,QB的方程,求得M,N的坐标,由此能导出以MN为直径的圆过两定点(-5b,0),(5b,0).
解答 解:(1)由已知得F2(3b,0),A($\frac{8}{3}$b,y0),
则直线F2A的方程为:y=-$\frac{3{y}_{0}}{b}$(x-3b),
令x=0得y=9y0,即P2(0,9y0),
设P(x,y),则$\left\{\begin{array}{l}{x=\frac{{x}_{0}}{2}}\\{y=\frac{{x}_{0}+9{y}_{0}}{2}=5{y}_{0}}\end{array}\right.$,
即$\left\{\begin{array}{l}{{x}_{0}=2x}\\{{y}_{0}=\frac{y}{5}}\end{array}\right.$代入$\frac{{{x}_{0}}^{2}}{8{b}^{2}}$-$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1得:$\frac{4{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{25{b}^{2}}$=1,
即P的轨迹E的方程为$\frac{{x}^{2}}{2{b}^{2}}$-$\frac{{y}^{2}}{25{b}^{2}}$=1.
(2)证明:在$\frac{{x}^{2}}{2{b}^{2}}$-$\frac{{y}^{2}}{25{b}^{2}}$=1中令y=0得x2=2b2,
则不妨设B(-$\sqrt{2}$b,0),D($\sqrt{2}$b,0),
于是直线QB的方程为:y=$\frac{{y}_{1}}{\sqrt{2}b+{x}_{1}}$(x+$\sqrt{2}$b),
∴直线QD的方程为:y=$\frac{{y}_{1}}{{x}_{1}-\sqrt{2}b}$(x-$\sqrt{2}$b),
则M(0,$\frac{\sqrt{2}b{y}_{1}}{{x}_{1}+\sqrt{2}b}$),N(0,$\frac{-\sqrt{2}b{y}_{1}}{{x}_{1}-\sqrt{2}b}$),
则以MN为直径的圆的方程为:x2+(y-$\frac{\sqrt{2}b{y}_{1}}{{x}_{1}+\sqrt{2}b}$)(y-$\frac{-\sqrt{2}b{y}_{1}}{{x}_{1}-\sqrt{2}b}$),
令y=0得:x2=$\frac{2{b}^{2}{{y}_{1}}^{2}}{{{x}_{1}}^{2}-2{b}^{2}}$,
而Q(x1,y1)在$\frac{{x}^{2}}{2{b}^{2}}$-$\frac{{y}^{2}}{25{b}^{2}}$=1上,则x12-2b2=$\frac{2}{25}$y12,
于是x=±5b,
即以MN为直径的圆过两定点(-5b,0),(5b,0).
点评 本题考查轨迹方程的求法和求证以MN为直径的圆过两定点.解题时要认真审题,熟练掌握圆锥曲线的性质,注意挖掘题设中的隐含条件,合理地进行等价转化.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | kπ+$\frac{π}{2}$(k∈Z) | B. | kπ(k∈Z) | C. | 2kπ+$\frac{π}{2}$(k∈Z) | D. | $\frac{1}{2}kπ$(k∈Z) |
| A. | 6项 | B. | 7项 | C. | 8项 | D. | 9项 |
| A. | [-$\frac{3}{2}$,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,3] | C. | [-$\frac{3\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$] | D. | [-$\frac{3\sqrt{3}}{2}$,3] |
| A. | 45° | B. | 135° | C. | 90° | D. | 60° |