题目内容
【题目】在平面直角坐标系xOy中,直线![]() 与抛物线y2=4x相交于不同的A,B两点,O为坐标原点.
与抛物线y2=4x相交于不同的A,B两点,O为坐标原点.
(1) 如果直线![]() 过抛物线的焦点且斜率为1,求
过抛物线的焦点且斜率为1,求![]() 的值;
的值;
(2)如果![]() ,证明:直线
,证明:直线![]() 必过一定点,并求出该定点.
必过一定点,并求出该定点.
【答案】(1)8;(2)证明见解析
【解析】试题分析:(Ⅰ)根据抛物线的方程得到焦点的坐标,设出直线与抛物线的两个交点和直线方程,是直线的方程与抛物线方程联立,得到关于y的一元二次方程,根据根与系数的关系,求出弦长;
(Ⅱ)设出直线的方程,同抛物线方程联立,得到关于y的一元二次方程,根据根与系数的关系表示出数量积,根据数量积等于﹣4,做出数量积表示式中的b的值,即得到定点的坐标.
试题解析:
(1)解, ![]() ,
, 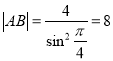
(2)证明 由题意:抛物线焦点为(1,0),设l:x=ty+b,代入抛物线y2=4x,
消去x得y2-4ty-4b=0,设A(x1,y1),B(x2,y2),则y1+y2=4t,y1y2=-4b,
∴![]() ·
·![]() =x1x2+y1y2=(ty1+b)(ty2+b)+y1y2 =t2y1y2+bt(y1+y2)+b2+y1y2
=x1x2+y1y2=(ty1+b)(ty2+b)+y1y2 =t2y1y2+bt(y1+y2)+b2+y1y2
=-4bt2+4bt2+b2-4b=b2-4b.
令b2-4b=-4,∴b2-4b+4=0,∴b=2,
∴直线l过定点(2,0).∴若![]() ·
·![]() =-4,则直线l必过一定点.
=-4,则直线l必过一定点.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目