Question

【题目】选修4—1：几何证明选讲

如图，已知AP是⊙O的切线，P为切点，AC是⊙O的割线，与⊙O交于B、C两点，圆心O在∠PAC的内部，点M是BC的中点.

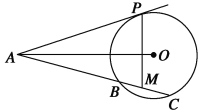
（1）证明：A、P、O、M四点共圆；

（2）求∠OAM＋∠APM的大小

Answer 1

【答案】（1）详见解析 （2） 90°

【解析】

试题分析：（1）证明四点共圆，一般利用对角互补进行证明：根据相切及垂径定理得OP⊥AP及OM⊥BC，从而得∠OPA＋∠OMA＝180°. （2）根据四点共圆得同弦所对角相等：∠OAM＝∠OPM，因此

∠OPM＋∠APM＝90°，

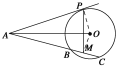
试题解析：（1）证明 连接OP，OM，因为AP与⊙O相切于点P，所以OP⊥AP.

因为M是⊙O的弦BC的中点，所以OM⊥BC，

于是∠OPA＋∠OMA＝180°.

由圆心O在∠PAC的内部，可知四边形APOM的对角互补，所以A、P、O、M四点共圆.

（2）解 由（1）得A、P、O、M四点共圆，

所以∠OAM＝∠OPM，

由（1）得OP⊥AP，因为圆心O在∠PAC的内部，

所以∠OPM＋∠APM＝90°，

所以∠OAM＋∠APM＝90°.