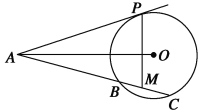
题目内容
【题目】已知直线![]() :
: ![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和点
和点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求定点![]() 的坐标;
的坐标;
(2)求圆![]() 的方程;
的方程;
(3)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点![]() ,问:在
,问:在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)直线过定点问题,应将直线![]() :
: ![]() 的方程中含
的方程中含![]() 的项合并,变为
的项合并,变为![]() ,解方程组
,解方程组![]() 即可求定点坐标;(2)方法一:设圆
即可求定点坐标;(2)方法一:设圆![]() 的一般方程为
的一般方程为![]() ,其圆心为
,其圆心为![]() ,由条件可得关于
,由条件可得关于![]() 三元方程组,解方程组可求解;方法二:设圆的方程为标准方程。(3)圆心C为
三元方程组,解方程组可求解;方法二:设圆的方程为标准方程。(3)圆心C为![]() 的中点,由中点坐标公式求点
的中点,由中点坐标公式求点![]() 的坐标。点M到圆心C距离大于半径,所以点M在圆C外。故
的坐标。点M到圆心C距离大于半径,所以点M在圆C外。故![]() 或
或![]() 为直角,两邻边垂直,斜率乘积为-1,可求m的值。
为直角,两邻边垂直,斜率乘积为-1,可求m的值。
试题解析:(1)由![]() 得,
得, ![]() ,
,
令![]() ,得
,得![]() ,即定点
,即定点![]() 的坐标为
的坐标为![]() .
.
(2)设圆![]() 的方程为
的方程为![]() ,
,
由条件得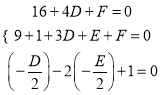 ,解得
,解得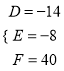 .
.
所以圆![]() 的方程为
的方程为![]() .
.
(3)圆![]() 的标准方程为
的标准方程为![]() ,
, ![]() ,
,
设点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,则有
,则有![]() ,
,
解得![]() ,
, ![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
因为![]() 在圆外,所以点
在圆外,所以点![]() 不能作为直角三角形的顶点,
不能作为直角三角形的顶点,
若点![]() 为直角三角形的顶点,则有
为直角三角形的顶点,则有![]() ,
, ![]() ,
,
若点![]() 是直角三角形的顶点,则有
是直角三角形的顶点,则有![]() ,
, ![]() ,
,
综上, ![]() 或
或![]() .
.
所以![]() ,
,
所以![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目