题目内容
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于
的距离之比等于![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为
所截得的线段的长为![]() ,求直线
,求直线![]() 的方程
的方程
【答案】 (1) ![]() 的轨迹方程是
的轨迹方程是![]() ,轨迹是以
,轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆;
为半径的圆;
(2) ![]() ,或
,或![]() .
.
【解析】 【试题分析】(1)运用两点间距离公式建立方程进行化简;(2)借助直线与圆的位置关系,运用圆心距、半径、弦长之间的关系建立方程待定直线的斜率,再用直线的点斜式方程分析求解:
(1)由题意,得 ![]()

化简,得![]() .
.
即![]() .
.
![]() 点
点![]() 的轨迹方程是
的轨迹方程是![]()
轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆
为半径的圆
(2)当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,
,
此时所截得的线段的长为![]() ,
,
![]() 符合题意.
符合题意.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为
![]() ,即
,即![]() ,
,
圆心到![]() 的距离
的距离![]() ,
,
由题意,得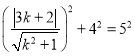 ,
,
解得![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
即![]() .
.
综上,直线![]() 的方程为
的方程为
![]() ,或
,或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目