题目内容
【题目】当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() .
.
【答案】详见解析
【解析】
试题分析:本题考查含参数一元二次不等式问题,由于![]() ,所以方程
,所以方程![]() 的两个实根分别为
的两个实根分别为![]() ,分三种情况进行讨论,当
,分三种情况进行讨论,当![]() ,即
,即![]() 时,结合相应函数图象可知,不等式的解集为
时,结合相应函数图象可知,不等式的解集为![]() ,当
,当![]() ,即
,即![]() 时,结合相应函数图象可知,不等式的解集为
时,结合相应函数图象可知,不等式的解集为![]() ,当
,当![]() ,即
,即![]() 时,结合相应函数图象可知,不等式的解集为
时,结合相应函数图象可知,不等式的解集为![]() ,本题主要考查分类讨论思想方法、考查数形结合思想方法,需要注意的是在对参数讨论时,要做到“不重不漏”,考查学生基本运算能力,属于常规考查.
,本题主要考查分类讨论思想方法、考查数形结合思想方法,需要注意的是在对参数讨论时,要做到“不重不漏”,考查学生基本运算能力,属于常规考查.
试题解析:由于a>0,所以原不等式可化为(x-2)(x-![]() )>0,
)>0,
由![]() =2可得a=1,
=2可得a=1,
当0<a<1时,解不等式可得x<2或x>![]() ;
;
当a=1时,解不等式得x∈R且x≠2;
当a>1时,解不等式得x<![]() 或x>2.
或x>2.
综上所述,当0<a<1时,原不等式的解集为{x|x>![]() 或x<2},
或x<2},
当a=1时,原不等式的解集为{x|x≠2},
当a>1时,原不等式的解集为{x|x>2或x<![]() }
}

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
【题目】为了了解我国各景点在大众中的熟知度,随机对![]() ~
~![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组[ | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
![]()
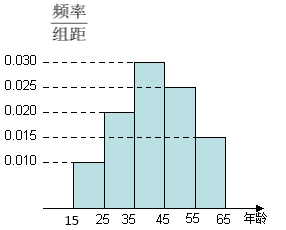
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组各抽取多少人;
组每组各抽取多少人;
(3)在(2)的条件下抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求所抽取的人中恰好没有第
人,求所抽取的人中恰好没有第![]() 组人的概率.
组人的概率.