题目内容
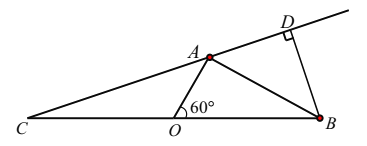
【题目】已知c>0,设命题p:函数![]() 为减函数.命题q:当
为减函数.命题q:当![]() 时,函数f(x)=x+
时,函数f(x)=x+![]() >
>![]() 恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
【答案】![]() ∪[1,+∞).
∪[1,+∞).
【解析】试题分析:先分别确定命题为真时参数取值范围:命题p为真知,0<c<1;命题q为真知,x+![]() 的最小值>
的最小值>![]() ,而2≤x+
,而2≤x+![]() ,即
,即![]() <2,再根据“p∨q”为真命题,“p∧q”为假命题,得p,q中必有一真一假,最后利用补集求命题为假时参数取值范围
<2,再根据“p∨q”为真命题,“p∧q”为假命题,得p,q中必有一真一假,最后利用补集求命题为假时参数取值范围
试题解析:由命题p为真知,0<c<1;由命题q为真知,2≤x+![]() ≤
≤![]() ,要使此式恒成立,需
,要使此式恒成立,需![]() <2,即c>
<2,即c>![]() ,若“p∨q”为真命题,“p∧q”为假命题,则p,q中必有一真一假,当p真q假时,c的取值范围是
,若“p∨q”为真命题,“p∧q”为假命题,则p,q中必有一真一假,当p真q假时,c的取值范围是![]() ;当p假q真时,c的取值范围是[1,+∞).
;当p假q真时,c的取值范围是[1,+∞).
综上可知,c的取值范围是![]() ∪[1,+∞).
∪[1,+∞).

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】为了了解我国各景点在大众中的熟知度,随机对![]() ~
~![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组[ | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
![]()
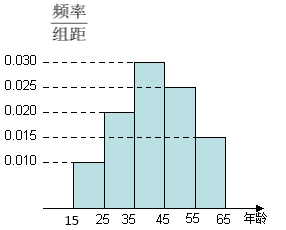
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组各抽取多少人;
组每组各抽取多少人;
(3)在(2)的条件下抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求所抽取的人中恰好没有第
人,求所抽取的人中恰好没有第![]() 组人的概率.
组人的概率.