��Ŀ����
1����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{{\sqrt{6}}}{3}$�����᳤Ϊ2$\sqrt{6}$����������ԲC�ı����̣�
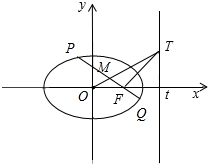
������FΪ��ԲC���ҽ��㣬TΪֱ��x=t��t��R��t��2���������겻Ϊ0������һ�㣬��F��TF�Ĵ��߽���ԲC�ڵ�P��Q��
��������OTƽ���߶�PQ������OΪ����ԭ�㣩����t��ֵ��
�������ڣ������������£���$\frac{|TF|}{|PQ|}$��Сʱ�����T�����꣮
���� ��1������$\frac{c}{a}$=$\frac{{\sqrt{6}}}{3}$��2a=2$\sqrt{6}$����a2=b2+c2��������ɣ�
��2���������ɣ�1���ɵã�F��������ǣ�2��0������ֱ��PQ�ķ���Ϊx=my+2������Բ����������Ϊ��m2+3��y2+4my-2=0������0����P��x1��y1����Q��x2��y2������MΪPQ���е㣬���ø���ϵ���Ĺ�ϵ�ɵã�M������꣮����TF��PQ���ɵ�ֱ��FT��б��Ϊ-m���䷽��Ϊy=-m��x-2�����ɵõ�T�����꣬��M���������������ɣ�
�������ɣ�����֪TΪֱ��x=3������һ��ɵã���T�������Ϊ��3��-m��������$|TF|=\sqrt{{m^2}+1}$��|PQ|=$\frac{{\sqrt{24}��{m^2}+1��}}{{{m^2}+3}}$������$\frac{|TF|}{|PQ|}$���û�������ʽ�����ʼ��ɵó���
���  �⣺��1����$\frac{c}{a}$=$\frac{{\sqrt{6}}}{3}$��2a=2$\sqrt{6}$����a2=b2+c2��
�⣺��1����$\frac{c}{a}$=$\frac{{\sqrt{6}}}{3}$��2a=2$\sqrt{6}$����a2=b2+c2��
���a2=6��b2=2��c=2��
����ԲC�ı�������$\frac{x^2}{6}+\frac{y^2}{2}=1$��
��2���������ɣ�1���ɵã�F��������ǣ�2��0����
��ֱ��PQ�ķ���Ϊx=my+2��
����$\left\{\begin{array}{l}{x=my+2}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$
��ȥx���ã�m2+3��y2+4my-2=0��
���б�ʽ��=16m2+8��m2+3����0��
��P��x1��y1����Q��x2��y2������y1+y2=$\frac{-4m}{m2+3}$��y1y2=$\frac{-2}{m2+3}$��
����x1+x2=m��y1+y2��+4=$\frac{12}{m2+3}$��
��MΪPQ���е㣬��M�������Ϊ$��\frac{6}{{{m^2}+3}}��\frac{-2m}{{{m^2}+3}}��$��
��TF��PQ��
��ֱ��FT��б��Ϊ-m���䷽��Ϊy=-m��x-2����
��x=tʱ��y=-m��t-2����
���T��������t��-m��t-2������
��ʱֱ��OT��б��Ϊ$\frac{{-m��{t-2}��}}{t}$���䷽��Ϊ$y=\frac{m��2-t��}{t}x$��
��M�������Ϊ$��\frac{6}{{{m^2}+3}}��\frac{-2m}{{{m^2}+3}}��$���룬��$\frac{-2m}{{{m^2}+3}}=\frac{m��2-t��}{t}•\frac{6}{{{m^2}+3}}$��
���t=3��
�������ɣ�����֪TΪֱ��x=3������һ��ɵã���T�������Ϊ��3��-m����
����$|TF|=\sqrt{{m^2}+1}$��|PQ|=$\frac{{\sqrt{24}��{m^2}+1��}}{{{m^2}+3}}$��
��$\frac{|TF|}{|PQ|}=\sqrt{{m^2}+1}•\frac{{{m^2}+3}}{{\sqrt{24}��{m^2}+1��}}=\frac{1}{{\sqrt{24}}}•\sqrt{\frac{{{{��{m^2}+3��}^2}}}{{{m^2}+1}}}$=$\frac{1}{{\sqrt{24}}}•\sqrt{\frac{{{{��{m^2}+3��}^2}}}{{{m^2}+1}}}=\frac{1}{{\sqrt{24}}}•\sqrt{\frac{{{{��{m^2}+1��}^2}+4��{m^2}+1��+4}}{{{m^2}+1}}}$=$\frac{1}{{\sqrt{24}}}•\sqrt{{m^2}+1+\frac{4}{{{m^2}+1}}+4}$$��\frac{1}{{\sqrt{24}}}•\sqrt{2\sqrt{4}+4}=\frac{{\sqrt{3}}}{3}$��
���ҽ���m2+1=$\frac{4}{m2+1}$����m=��1ʱ���Ⱥų�������ʱ$\frac{|TF|}{|PQ|}$ȡ����Сֵ$\frac{{\sqrt{3}}}{3}$��
�ʵ�$\frac{|TF|}{|PQ|}$��Сʱ��T��������ǣ�3��1����3��-1����
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ����ת��Ϊ���������ɵá���0�������ϵ���Ĺ�ϵ���ҳ���ʽ����������ʽ�����ʡ����ֱ��ֱ��б��֮��Ĺ�ϵ�Ȼ���֪ʶ��������ܷ�������������������������������������⣮

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
 ��ͼ������N��0��1����M��m��-1����m��0���Ķ�ֱ��l��������C��x2=2py����P��Q���㣨��P��M��N֮�䣩��OΪ����ԭ�㣮
��ͼ������N��0��1����M��m��-1����m��0���Ķ�ֱ��l��������C��x2=2py����P��Q���㣨��P��M��N֮�䣩��OΪ����ԭ�㣮