Question

10．画出函数y=x-2sinx，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]的大致图象．

Answer 1

分析 由题意可得函数图象过原点，图象关于原点对称，利用导数求得函数的单调区间，再结合正弦函数的图象特征，从而得到函数y=x-2sinx，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]的大致图象．

解答 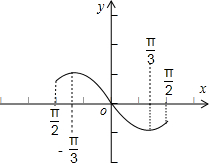解：当x=0时，y=0-2sin0=0，
故函数图象过原点，再由f（-x）=-f（x）图象关于原点对称，
又∵y'=1-2cosx，令y′=0，求得cosx=$\frac{1}{2}$，
结合x∈[-$\frac{π}{2}$，$\frac{π}{2}$]，可得x±$\frac{π}{3}$，
故函数的单调区间以±$\frac{π}{3}$为分界点．
在[-$\frac{π}{3}$，$\frac{π}{3}$]上，y′＜0，函数y为减函数；
在[-$\frac{π}{2}$，-$\frac{π}{3}$]、[$\frac{π}{3}$，$\frac{π}{2}$]上，y′＞0，函数y为增函数；
如图所示．

点评 本题主要考查函数的奇偶性、单调性，正弦函数的图象特征，属于基础题．