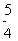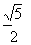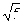题目内容
如图,过抛物线 的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 ( )
的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 ( )
A. B.
B. C.
C. D.
D.
B
解析试题分析:如图分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,则由已知得:|BC|=2a,
由定义得:|BD|=a,故∠BCD=30°,
在直角三角形ACE中,∵|AE|=3,|AC|=3+3a,
∴2|AE|=|AC|, 3+3a=6,从而得a=1。
∵BD∥FG,∴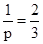 ,p=
,p=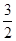 ,因此抛物线方程为y2=3x.故选B.
,因此抛物线方程为y2=3x.故选B.
考点:本题主要考查抛物线的定义及其几何性质,相似三角形。
点评:小综合题,本题综合性较强,综合考查抛物线的定义、标准方程、几何性质,以及平面几何知识。一般的涉及抛物线过焦点弦问题,要考虑应用定义。

练习册系列答案
相关题目
直线 与曲线
与曲线 的交点个数为( )
的交点个数为( )
| A.4个 | B.1个 | C.2个 | D.3个 |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A. | B. | C.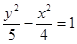 | D. |
抛物线 的焦点F是椭圆
的焦点F是椭圆 的一个焦点,且它们的交点M到F的距离为
的一个焦点,且它们的交点M到F的距离为 ,则椭圆的离心率为
,则椭圆的离心率为
A. | B. | C. | D. |
如图, 是平面
是平面 的斜线段,
的斜线段, 为斜足。若点
为斜足。若点 在平面
在平面 内运动,使得
内运动,使得 的面积为定值,则动点
的面积为定值,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 |
| C.一条直线 | D.两条平行直线 |
曲线 +
+ =1.(m<6) 与
=1.(m<6) 与 +
+ =1.(5<m<9)的( )
=1.(5<m<9)的( )
| A.准线相同 | B.离心率相同 | C.焦点相同 | D.焦距相同 |
 和双曲线
和双曲线 有相同的焦点F1、F2,以线段F1F2为边作正△F1F2M,若椭圆与双曲线的一个交点P恰好是MF1的中点,设椭圆和双曲线的离心率分别为
有相同的焦点F1、F2,以线段F1F2为边作正△F1F2M,若椭圆与双曲线的一个交点P恰好是MF1的中点,设椭圆和双曲线的离心率分别为 等于
等于 的双曲线与圆
的双曲线与圆 的一个交点,则
的一个交点,则 = ( )
= ( )



 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x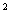 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ).