题目内容
15．函数y=${2}^{\sqrt{x-2}}$-log3（5-x）的值域为[0，+∞）．分析 根据函数的解析式求出定义域，再根据单调性求得它的值域．
解答 解：由函数y=${2}^{\sqrt{x-2}}$-log3（5-x），可得2≤x＜5，故函数的定义域为[2，5），
且函数在它的定义域内单调递增，故当x=2时，函数取得最小值为20-1=0，
当x趋于5时，函数值趋于+∞，故函数的值域为[0，+∞），
故答案为：[0，+∞）．
点评 本题主要考查函数的定义域和单调性的应用，求函数的值域，属于基础题．
练习册系列答案
相关题目
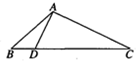如图，在△ABC中，已知点D在BC边上，AD⊥AC，sin∠BAC=$\frac{2\sqrt{2}}{3}$，AB=3$\sqrt{2}$，AD=3，求BD的长．