题目内容
设函数f(x)=x2+x-.
(1)若函数的定义域为[0,3],求f(x)的值域;
(2)若定义域为[a,a+1]时,f(x)的值域是[-,],求a的值
(1)∵f(x)=2-,
∴对称轴为x=-.
∵-<0≤x≤3,
∴f(x)的值域是[f(0),f(3)],
即.
(2)∵f(x)的最小值为-,
∴对称轴
x=-∈[a,a+1].
∴
解得-≤a≤-.
∵区间[a,a+1]的中点为
x0=a+,
当a+≥-,
即-1≤a≤-时,
f(x)最大值为f(a+1)=.
∴(a+1)2+(a+1)-
=.
∴16a2+48a+27=0.
∴a=-.
当a+<-,
即-≤a<-1时,
f(x)最大值为f(a)=,
∴a2+a-=.
∴16a2+16a-5=0.
∴a=-.
综上知a=-
或a=-.
解析

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
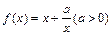 ,
,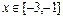 时,
时,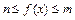 恒成立,求
恒成立,求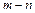 的最小值.
的最小值.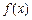 满足
满足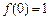 ,
,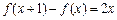 .
.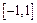 上的最大值和最小值.
上的最大值和最小值.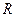 上的函数
上的函数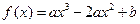
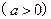 在区间
在区间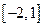 上的最大值是
上的最大值是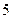 ,最小值是
,最小值是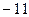 .
.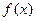 的解析式;
的解析式;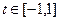 时,
时,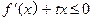 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.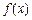 在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数
在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数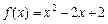 在[1,2]上是否具有“DK”性质,说明理由;
在[1,2]上是否具有“DK”性质,说明理由;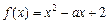 在[a,a+1]上具有“DK”性质,求a的取值范围.
在[a,a+1]上具有“DK”性质,求a的取值范围.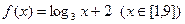 ,求函数
,求函数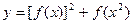 的最大值。
的最大值。 数
数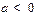 , 设函数
, 设函数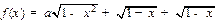 的最大值为
的最大值为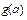 。
。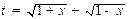 ,求
,求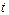 的取值范围,并把
的取值范围,并把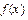 表示为
表示为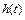 ;
;