题目内容
若函数y=f(x)=x2-2x+4的定义域、值域都是闭区间[2,2b],求b的值.
∵y=f(x)=(x2-4x+8)=(x-2)2+2,
∴其图象的对称轴是x=2.
因此y=f(x)在[2,2b]上是递增函数,且2b>2,即b>1.
又函数y=f(x)=x2-2x+4的定义域、值域都是闭区间[2,2b],所以有f(2b)=2b,即(2b)2-2×2b+4=2b,
∴b2-3b+2=0,∴b=1(舍去),b=2.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
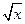 -2(x≥0)及f2(x)=4-6·
-2(x≥0)及f2(x)=4-6·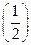 x(x≥0)是否属于集合A?并简要说明理由;
x(x≥0)是否属于集合A?并简要说明理由;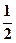 ,1]时,不等式f (ax+1)≤f (x-2)恒成立,则求实数a的取值范围?
,1]时,不等式f (ax+1)≤f (x-2)恒成立,则求实数a的取值范围? 。设
。设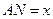 (单位:米),若
(单位:米),若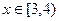 (单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。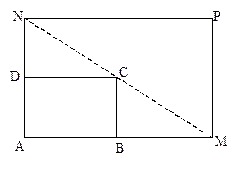
 (升)关于行驶速度x(千米/小时)的函数解析式可以表示为:
(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: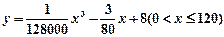 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。 速行驶时,从甲地到乙地要耗油多少升?
速行驶时,从甲地到乙地要耗油多少升? ,
,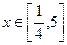 , 其中
, 其中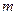 是不等于零的常数,
是不等于零的常数, 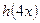 的定义域(2分);
的定义域(2分);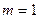 时,直接写出
时,直接写出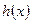 的值域(4分)
的值域(4分)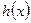 的单调递增区间(理5分,文8分);
的单调递增区间(理5分,文8分);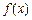
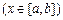 ,定义:
,定义: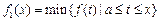

 表示函数
表示函数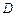 上的最小值,
上的最小值,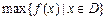 表示函数
表示函数 上的最大值.例如:
上的最大值.例如: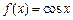 ,
,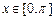 ,则
,则 ,
,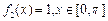 ,
,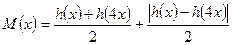 ,不等式
,不等式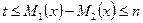
 的取值范围(11分);
的取值范围(11分);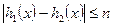 恒成立,求
恒成立,求 的取值范围(8分);
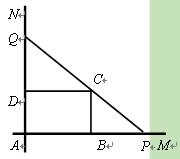
的取值范围(8分); 直的两条公路
直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个
,现欲将其扩建成一个 更大的三角形花园
更大的三角形花园 ,要求
,要求 在射线
在射线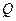 在射线
在射线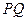 过点
过点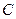 ,其中
,其中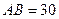 米,
米,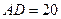 米. 记三角形花园
米. 记三角形花园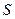 .
.
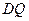
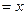 米,将
米,将 的函数.
的函数. 当
当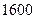 平方米,则
平方米,则