题目内容
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米![]() 微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某试点城市环保局从该市市区2019年上半年每天的
微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某试点城市环保局从该市市区2019年上半年每天的![]() 监测数据中随机的抽取15天的数据作为样本,监测值如下茎叶图所示(十位为茎,个位为叶).
监测数据中随机的抽取15天的数据作为样本,监测值如下茎叶图所示(十位为茎,个位为叶).
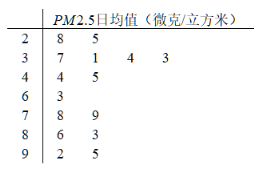
(1)在这15天的![]() 日均监测数据中,求其中位数;
日均监测数据中,求其中位数;
(2)从这15天的数据中任取2天数据,记![]() 表示抽到
表示抽到![]() 监测数据超标的天数,求
监测数据超标的天数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)以这15天的![]() 日均值来估计该市下一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级.
日均值来估计该市下一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级.
【答案】(1)45;(2)分布列见解析,![]() ;(3)219.
;(3)219.
【解析】
(1)由茎叶图从小到大找到第8个数,即为中位数;
(2)由于假设记“从15天的PM2.5日均监测数据中,随机抽出2天,超标的有6天,未超标的有9天,![]() 服从超几何分布,求出
服从超几何分布,求出![]() 分别取
分别取![]() 的概率,列出分分列,求出数学期望;
的概率,列出分分列,求出数学期望;
(3)先计算一年中每天空气质量达到一级或二级的概率,则一年中空气质量达到一级或二级的天数为![]() 服从二项分布,根据二项分布的期望公式求出期望.
服从二项分布,根据二项分布的期望公式求出期望.
(1)由茎叶图可得中位数是45.
(2)依据条件,![]() 服从超几何分布:
服从超几何分布:
其中![]() ,
,![]() ,
,![]() ,
,![]() 的可能值为
的可能值为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
P |
|
|
|
![]() .
.
(3)依题意可知,一年中每天空气质量达到一级或二级的概率为![]() ,
,
一年中空气质量达到一级或二级的天数为![]() ,
,
则![]() ,
,![]() ,
,
∴一年中平均有219天的空气质量达到一级或二级.

【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中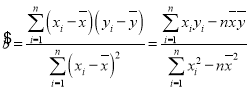 ,
,![]() ,
, .
.