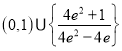题目内容
【题目】甲、乙、丙三人参加竞答游戏,一轮三个题目,每人回答一题为体现公平,制定如下规则:
①第一轮回答顺序为甲、乙、丙;第二轮回答顺序为乙、丙、甲;第三轮回答顺序为丙,甲、乙;第四轮回答顺序为甲、乙、丙;…,后面按此规律依次向下进行;
②当一人回答不正确时,竞答结束,最后一个回答正确的人胜出.
已知,每次甲回答正确的概率为![]() ,乙回答正确的概率为
,乙回答正确的概率为![]() ,丙回答正确的概率为
,丙回答正确的概率为![]() ,三个人回答每个问题相互独立.
,三个人回答每个问题相互独立.
(1)求一轮中三人全回答正确的概率;
(2)分别求甲在第一轮、第二轮、第三轮胜出的概率;
(3)记![]() 为甲在第
为甲在第![]() 轮胜出的概率,
轮胜出的概率,![]() 为乙在第
为乙在第![]() 轮胜出的概率,求
轮胜出的概率,求![]() 与
与![]() ,并比较
,并比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)![]() ;(2)甲在第一轮胜出的概率为
;(2)甲在第一轮胜出的概率为![]() ;甲在第二轮胜出的概率为
;甲在第二轮胜出的概率为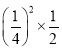 ;甲在第三轮胜出的概率为
;甲在第三轮胜出的概率为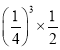 ;(3)答案见解析.
;(3)答案见解析.
【解析】
(1)由事件的独立性可求出一轮中三人全回答正确的概率.
(2)列举出三种情况下甲乙丙三人的胜负情况,结合事件的独立性即可求出概率.
(3)通过计算![]() 时甲、乙胜的概率,总结规律,求出
时甲、乙胜的概率,总结规律,求出![]() ,
,![]() ,进而可比较二者的大小关系.
,进而可比较二者的大小关系.
解:(1)设一轮中三人全回答正确为事件![]() ,则
,则![]() .
.
(2)甲在第一轮胜出的概率为![]() ;
;
甲在第二轮胜出的概率为![]() ;
;
甲在第三轮胜出的概率为![]() .
.
(3)由(2)知![]() ;
;![]() ;
;![]() .
.
由题意得![]() ;
;![]() ;
;
![]() ;
;![]()
….
所以,当![]() (
(![]() )时,
)时,![]() .
.
当![]() (
(![]() )时,
)时,![]() ;
;
当![]() (
(![]() )时,
)时,![]() .
.
同理可得,当![]() (
(![]() )时,
)时,![]() ;
;
当![]() (
(![]() )时,
)时,![]() ;
;
当![]() (
(![]() )时,
)时,![]() .
.
所以,当![]() (
(![]() )时,
)时,![]() ;当
;当![]() (
(![]() )时,
)时,![]() ;
;
当![]() (
(![]() )时,
)时,![]() ;
;

练习册系列答案
相关题目