题目内容
【题目】棱长为1的正方体
内部有一圆柱
，此圆柱恰好以直线
为轴.有下列命题：
①圆柱的母线与正方体所有的棱所成的角都相等；
②正方体所有的面与圆柱的底面所成的角都相等；
③在正方体内作与圆柱底面平行的截面，则截面的面积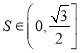
；
④圆柱侧面积的最大值为
.
其中正确的命题是______.
【答案】①②④
【解析】
根据正方体的特性分析可知①②正确，作出一个与圆柱底面平行的截面，举出反例得到③错误，利用几何法找出圆柱的底面半径，列式计算圆柱侧面积，结合均值不等式计算得到④正确，得到答案.
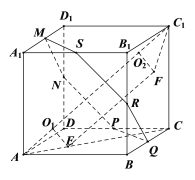
如图所示：易知圆柱
的母线与
平行，由正方体的对称性可知与其每条侧棱间的夹角都相等，①正确；
设
分别为对应棱的中点，易知共面，
易证
，
，则
平面
，
平面，故
，同理可得
，故
平面
，
又圆柱的底面与垂直，
故平面与圆柱的底面平行，
根据正方体的特点可知，平面与正方体所有侧面的夹角相同，
故正方体
所有的面与圆柱的底面所成的角都相等，②正确；
此时截面的面积为
，③错误；
设圆柱底面半径为
，则圆柱的底面必与过
点的三个面相切，
且切点分别在线段
上，设在
上的切点为
，
为圆柱的一条高，
根据对称性知：
，则圆柱的高为
，
，
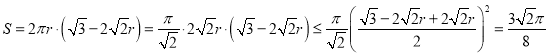当
，即
时等号成立，④正确.
故答案为：①②④.
练习册系列答案
全优点练单元计划系列答案
相关题目
