题目内容
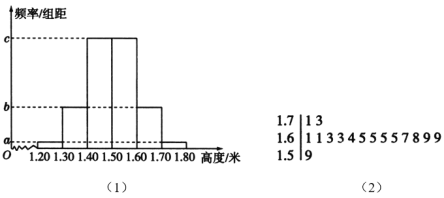
【题目】某公司订购了一批树苗,为了检测这批树苗是否合格,从中随机抽测100株树苗的高度,经数据处理得到如图(1)所示的频率分布直方图,其中最高的16株树苗的高度的茎叶图如图(2)所示,以这100株树苗的高度的频率估计整批树苗高度的概率.
(1)求这批树苗的高度高于![]() 米的概率,并求图(1)中
米的概率,并求图(1)中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批树苗中随机选取3株,记![]() 为高度在
为高度在![]() 的树苗数量,求
的树苗数量,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批树苗的高度满足近似于正态分布
的概率分布.如果这批树苗的高度满足近似于正态分布![]() 的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗能否被签收?
的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗能否被签收?
【答案】(1)概率为![]() ,
,![]() ,
,![]() ,
,![]() ;(2)分布列答案见解析,数学期望
;(2)分布列答案见解析,数学期望![]() ;(3)被签收.
;(3)被签收.
【解析】
(1)结合茎叶图,求得每组频率,再求得![]() 的值.
的值.
(2)根据二项分布的知识求得分布列并求得数学期望.
(3)求得![]() 与
与![]() ,由此判断这批树苗的高度满足近似于正态分布
,由此判断这批树苗的高度满足近似于正态分布![]() 的概率分布,应认为这批树苗是合格的,能被签收.
的概率分布,应认为这批树苗是合格的,能被签收.
(1)由题图(2)可知,100株样本树苗中高度高于![]() 米的共有15株,
米的共有15株,
以样本的频率估计总体的概率,可得这批树苗的高度高于![]() 米的概率为
米的概率为![]() .
.
记![]() 为树苗的高度,结合题图(1)(2)可得:
为树苗的高度,结合题图(1)(2)可得:
![]() ,
,
![]() ,
,
![]() .
.
因为组距为![]() ,所以
,所以![]() ,
,![]() ,
,![]() .
.
(2)以样本的频率估计总体的概率,可得:从这批树苗中随机选取1株,高度在![]() 的概率为
的概率为
![]() .
.
因为从这批树苗中随机选取3株,相当于三次独立重复试验,
所以随机变量![]() 服从二项分布
服从二项分布![]() ,
,
故![]() 的分布列为
的分布列为![]() ,
,
即
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() (或
(或![]() ).
).
(3)由![]() ,取
,取![]() ,
,![]() ,
,
由(2)可知,![]() ,
,
又结合(1),可得![]()
![]()
![]() ,
,
所以这批树苗的高度满足近似于正态分布![]() 的概率分布,
的概率分布,
应认为这批树苗是合格的,将顺利被该公司签收.

练习册系列答案
相关题目