题目内容
4.已知m、n是两条不重合的直线,α、β是两个不重合的平面,给出下列命题;①若m?α,n?β,m∥n,则α∥β;②若m、n是异面直线,m∥β,n?β,n∥α,则α∥β.其中( )| A. | ①②都是真命题 | B. | ①②都是假命题 | ||
| C. | ①是真命题,②是假命题. | D. | ①是假命题,②是真命题. |
分析 ①根据面面平行的判定定理进行判断即可.
②根据面面平行的判定定理进行判断即可.
解答  解:①如图:m?α,n?β,m∥n,则α∥β或相交,故①错误;
解:①如图:m?α,n?β,m∥n,则α∥β或相交,故①错误;
②若m、n是异面直线,m∥β,n?β,n∥α,则α∥β,正确,
故选:D.
点评 本题主要考查空间直线和平面位置关系的判断,比较基础.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
16. 单位正方体ABCD-A1B1C1O在空间直角坐标系中的位置如图所示,动点M(a,a,0),N(0,b,1),其中0≤a≤1,0≤b≤1.设由M,N,O三点确定的平面截该正方体的截面为E,那么( )
单位正方体ABCD-A1B1C1O在空间直角坐标系中的位置如图所示,动点M(a,a,0),N(0,b,1),其中0≤a≤1,0≤b≤1.设由M,N,O三点确定的平面截该正方体的截面为E,那么( )
 单位正方体ABCD-A1B1C1O在空间直角坐标系中的位置如图所示,动点M(a,a,0),N(0,b,1),其中0≤a≤1,0≤b≤1.设由M,N,O三点确定的平面截该正方体的截面为E,那么( )
单位正方体ABCD-A1B1C1O在空间直角坐标系中的位置如图所示,动点M(a,a,0),N(0,b,1),其中0≤a≤1,0≤b≤1.设由M,N,O三点确定的平面截该正方体的截面为E,那么( )| A. | 对任意点M,存在点N使截面E为三角形 | |
| B. | 对任意点M,存在点N使截面E为正方形 | |
| C. | 对任意点M和N,截面E都是梯形 | |
| D. | 对任意点N,存在点M使得截面E为矩形 |
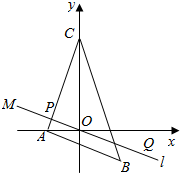 如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.
如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.