题目内容
9．已知曲线C：y=4ax3+x，过点Q（0，-1）作C的切线l，切点为P．（1）求证：不论a怎样变化．点P总-在一条定直线上；
（2）若a＞0，过点P且与1垂直的直线与x轴交于点T，求OT的最小值（0为坐标原点）．
分析 （1）设P（x0，y0），求出函数的导数，求得切线的斜率，再由两点的斜率公式，计算即可得证；
（2）运用两直线垂直的条件：斜率之积为-1，再由直线方程的点斜式，可得PT的方程，令y=0，可得|OT|，再由基本不等式可得最小值．
解答 （1）证明：设P（x0，y0），则y0=4ax03+x0，
由y=4ax3+x的导数为y′=12ax2+1，
则以P为切点的切线的斜率为k=12ax02+1，
由于切线经过切点（0，-1），
可得切线的斜率为$\frac{{y}_{0}+1}{{x}_{0}}$=$\frac{4a{{x}_{0}}^{3}+{x}_{0}+1}{{x}_{0}}$=12ax02+1，
解得x0=$\frac{1}{2\root{3}{a}}$，即有y0=4ax03+x0=x0+$\frac{1}{2}$，
则切点P总在直线y=x+$\frac{1}{2}$上；
（2）解：由l的斜率为$\frac{{y}_{0}+1}{{x}_{0}}$，可得PT的斜率为-$\frac{{x}_{0}}{{y}_{0}+1}$，
则PT的方程为y-y0=-$\frac{{x}_{0}}{{y}_{0}+1}$（x-x0），
令y=0，可得PT与x轴交点的横坐标为x=x0+$\frac{{y}_{0}（{y}_{0}+1）}{{x}_{0}}$=2+2x0+$\frac{3}{4{x}_{0}}$，
在（1）中，x0=$\frac{1}{2\root{3}{a}}$，又a＞0，则x0＞0，
则|OT|=2+2x0+$\frac{3}{4{x}_{0}}$≥2+2$\sqrt{2{x}_{0}•\frac{3}{4{x}_{0}}}$=2+$\sqrt{6}$，
当且仅当2x0=$\frac{3}{4{x}_{0}}$，即有x0=$\frac{\sqrt{6}}{4}$，等号成立，
则OT的最小值为2+$\sqrt{6}$．
点评 本题考查导数的运用：求切线方程，考查两直线垂直的条件，考查基本不等式的运用，化简整理的运算能力，属于中档题．
期末冲刺100分创新金卷完全试卷系列答案| A． | ①②都是真命题 | B． | ①②都是假命题 | ||
| C． | ①是真命题，②是假命题． | D． | ①是假命题，②是真命题． |
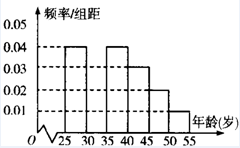某班同学在暑假期间进行社会实践活动，从本地[25，55]岁的人群中随机抽取n人进行了一次有关“房地产投资”的调查，得到如下统计数据和频率分布直方图：
| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组 | [25，30） | 120 | 0.6 |
| 第二组 | [30，35） | 195 | P |
| 第三组 | [35，40） | 100 | 0.5 |
| 第四组 | [40，45） | a | 0.4 |
| 第五组 | [45，50） | 30 | 0.3 |
| 第六组 | [50，55] | 15 | 0.3 |
（Ⅱ）从年龄在[40，50）岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动，并从中选取3人作为代表发言，记选取的3名代表中年龄在
[40，45）岁的人数为X，求X的分布列和数学期望．