题目内容
【题目】解方程ln（2x+1）=ln（x2﹣2）；
求函数f（x）=（ 
）2x+2×（ ）x（x≤﹣1）的值域．
【答案】解：由题意：ln（2x+1）=ln（x2﹣2）；
所以有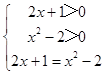 
x=3 或﹣1（负舍）
故方程的解为{x|x=3}；
函数f（x）=（ 
）2x+2×（ ）x（x≤﹣1）
令t= 
∈[2，+∞），换元后得：
g（t）=t2+2t （t≥2）
g（t）为一元二次函数，开口朝上，对称轴为t=﹣1，知：
g（t）在（2，+∞）上单调递增，g（t）min=8
故g（t）的值域为[8，+∞）
【解析】（1）根据方程式，方程的解需要满足函数定义域要求，再根据对数相等即可列出方程式；（2）利用换元法转化为一元二次函数来求原函数的值域即可；
【考点精析】认真审题，首先需要了解函数的值域(求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的)，还要掌握对数的运算性质(①加法：
②减法：
③数乘：
④
⑤
)的相关知识才是答题的关键．
练习册系列答案
名校课堂系列答案
相关题目
