Question

3．已知a∈R，函数f（x）=x|x-2a|．
（1）当a=1时，写出函数y=f（x）的单调递增区间；
（2）当a＞2时，求函数y=f（x）在区间[1，2]上的最小值；
（3）设a≠0，若函数y=f（x）在（m，n）上既有最大值又有最小值，请分别求出m、n的取值范围．（用a表示）

Answer 1

分析 （1）通过a=1可知f（x）的解析式，利用图象即得结论；
（2）通过a＞2、x∈[1，2]可知f（x）=-（x-a）²+a²，利用区间[1，2]在x=a的左边可知f（x）_min=f（1）；
（3）通过f（x）=$\left\{\begin{array}{l}{x（x-2a），}&{x≥2a}\\{x（2a-x），}&{x＜2a}\end{array}\right.$，分a＞0、a＜0两种情况讨论即可．

解答 解：（1）当a=1时，f（x）=x|x-2|=$\left\{\begin{array}{l}{（x-1）^{2}-1，}&{x≥2}\\{-（x-1）^{2}+1，}&{x＜2}\end{array}\right.$，
∵f（x）=（x-1）²-1的图象时开口向上，对称轴x=1的抛物线，
f（x）=-（x-1）²+1的图象时开口向下，对称轴x=1的抛物线，
∴当x≤1时或x≥2时，y=f（x）单调递增，
故函数y=f（x）的单调递增区间为：（-∞，1]∪[2，+∞）；
（2）∵a＞2，x∈[1，2]，
∴f（x）=x（2a-x）=-x²+2ax=-（x-a）²+a²，
又∵区间[1，2]在x=a的左边，
∴f（x）_min=f（1）=2a-1；
（3）依题意，f（x）=$\left\{\begin{array}{l}{x（x-2a），}&{x≥2a}\\{x（2a-x），}&{x＜2a}\end{array}\right.$，
①当a＞0时，如下图左所示，
由$\left\{\begin{array}{l}{y={a}^{2}}\\{y=x（x-2a）}\end{array}\right.$，解得：x=（1+$\sqrt{2}$）a，
∴0≤m＜a，2a＜n≤（1+$\sqrt{2}$）a；
②当a＜0时，如下图右所示，
由$\left\{\begin{array}{l}{y=-{a}^{2}}\\{y=x（2a-x）}\end{array}\right.$，解得：x=（1+$\sqrt{2}$）a，
∴（1+$\sqrt{2}$）a≤m＜2a，a＜n≤0．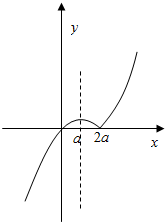
       

点评 本题考查分段函数的应用，考查分类讨论的思想，注意解题方法的积累，属于中档题．