题目内容
已知x,y为正实数,满足1≤lg(xy)≤2,3≤lg ≤4,求lg(x4y2)的取值范围.
≤4,求lg(x4y2)的取值范围.
6≤lg(x4y2)≤10
【解析】设a=lgx,b=lgy,则lg(xy)=a+b,
lg =a-b,lg(x4y2)=4a+2b,
=a-b,lg(x4y2)=4a+2b,
设4a+2b=m(a+b)+n(a-b),
∴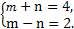 解得
解得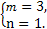
∴lg(x4y2)=3lg(xy)+lg ,
,
∵3≤3lg(xy)≤6,3≤lg ≤4,∴6≤lg(x4y2)≤10.
≤4,∴6≤lg(x4y2)≤10.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
题目内容
已知x,y为正实数,满足1≤lg(xy)≤2,3≤lg ≤4,求lg(x4y2)的取值范围.
≤4,求lg(x4y2)的取值范围.
6≤lg(x4y2)≤10
【解析】设a=lgx,b=lgy,则lg(xy)=a+b,
lg =a-b,lg(x4y2)=4a+2b,
=a-b,lg(x4y2)=4a+2b,
设4a+2b=m(a+b)+n(a-b),
∴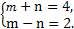 解得
解得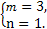
∴lg(x4y2)=3lg(xy)+lg ,
,
∵3≤3lg(xy)≤6,3≤lg ≤4,∴6≤lg(x4y2)≤10.
≤4,∴6≤lg(x4y2)≤10.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案